张海刚^1，2) ，张森^1，2) ，尹怡欣^1，2)

1) 北京科技大学自动化学院，北京100083 2) 北京科技大学钢铁流程先进控制教育部重点实验室，北京100083

摘 要  针对高炉故障诊断系统快速性和准确性的要求，提出基于全局优化最小二乘支持向量机的策略． 首先，采用变尺度离散粒子群对最小二乘支持向量机的参数和故障特征的选取进行优化; 然后，利用核主元分析法对选取的特征向量进行压缩整理; 最后，构造了以Fisher 线性判别率为标准的启发式纠错输出编码． 仿真结果表明，通过对故障训练样本有意义地分割重组，用较少的最小二乘支持向量机分类器，得到较高的故障判断准确率且增强了整个系统的实时性．

关 键 词  高炉; 故障诊断; 最小二乘分析; 支持向量机; 全局优化

钢铁工业是我国国民经济的基础产业和支柱产业^［1］． 高炉炼铁在钢铁工业中处于举足轻重的地位．高炉炼铁系统生产设备繁多，具有多耦合、大延时、非线性等特点． 尽管在高炉本体上安装了很多自动化的检测装置，然而由于高炉运行炉况复杂，无法建立准确的机理模型，在高炉自动控制决策过程中，仍将其当为“黑箱”系统进行处理． 高炉生产追求稳定，稳定炉况不仅能够保证铁水质量，而且能够提高煤气利用率，达到节能减排的目的． 高炉炉况故障诊断在高炉自动化控制的研究中一直是热点话题，准确及时的故障诊断技术能够确定高炉的稳定生产，降低故障所带来的经济损失^［2］．

在高炉生产中，由于缺少准确的机理模型，往往从数据驱动角度建立高炉故障诊断模型^［3］． 基于专家系统的故障诊断方法，计算机模仿专家经验，进行故障决策^［4］． 虽然引进国外的专家系统有一定的效果，但是其价格昂贵，并且国内大多数高炉检测设备落后，操作管理水平低，造成重要参数的数据不完整，不准确，导致国外专家系统难以适合我国国情． 文献^［5］基于人工神经网络建立了高炉故障诊断模型，取得了不错的效果． 但由于其建立在大数定理的渐近理论之上，要求学习样本足够多，收敛速度比较慢且容易陷入局部极值或过学习的困境，在实际应用中隐含层的层数及每层神经元数目如何确定也无规律可循． 李振^［6］将贝叶斯技术运用到高炉故障诊断中，设计了因果关系贝叶斯网络诊断模型． 然而高炉的智能故障诊断面临的是典型故障样本少、特征参数呈非线性耦合且维数较高的模式识别难题，所建立的贝叶斯模型往往达不到期望的精度． 除此之外，高炉处于复杂的工业生产环境中，样本数据往往受到噪声干扰，这要求故障诊断算法有很强的鲁棒性． 高炉故障具有不同的形式，属于多分类问题，设计合理有效的故障检测分类器至关重要． 同时高炉生产对于故障检测的及时性也有一定的要求^［5］，及时准确的进行故障检测报警，不仅能够减少损失，而且能够保证高炉顺行，延长高炉寿命．

本文针对冶炼过程中出现的悬料、崩料和管道行程三种典型故障，提出基于全局优化支持向量机的多类别高炉故障诊断方法． 一方面，在智能故障诊断系统的构建过程中，为了降低特征空间的维数，减少存储空间的占用，提高机器学习的效率，需要对高炉的故障特征参数进行自动的筛选． 在数据预处理阶段，我们采用核主成分分析( kernel principal component analysis，KPCA) 方法对高炉故障特征数据进行降维处理，保留和高炉故障关联性较高的特征数据，提高检测准确率． 另外核函数的参数选择和支持向量机的惩罚因子影响着故障诊断系统的训练效果，为了避免人为设定参数的弊端，需要系统自发地对参数的最优值进行寻找． 本文在粒子群算法^［7］的基础上，提出变尺度离散粒子群参数优化方法，通过加强最优粒子的影响力，增强了系统的稳定性． 另一方面，高炉故障诊断本质上是多类别分类问题，而支持向量机是针对二元分类问题的学习方法，通常的处理方式是将复杂的多元分类问题分解为多个简单的二元分类问题． 纠错输出编码是一种分解重组多元分类问题的通用方法，其中一对多、密集随机编码法与一对一、稀疏随机编码法分别是经典的二元和三元编码方法的实例^［7］． 然而，以上方法的编码矩阵是预先定义好的，在编码矩阵的创建过程中，没有考虑到训练样本的数据特征，使得训练过程具有一定的盲目性． 本文采用以Fisher 线性判别率为标准的启发式纠错输出编码，该方法具有两个方面的优势: 首先，启发式的编码过程允许类集合按照最大的判别率重新组织，从而使编码矩阵的拓扑结构同一对一和一对多方法固定的方式相比变得更加灵活． 其次，与随机策略需要大量的分类器相比，有意义的重组显著减少了分类器的数量，从而得到较好的性能且提高了训练的速度．

我们首先详细介绍本文提出的全局优化最小二乘支持向量机分类算法，其次我们建立高炉智能故障诊断模型，最后展示基于真实生产数据的故障仿真结果．

1   基于全局优化最小二乘支持向量机的多类别分类方法

1. 1 最小二乘支持向量机

支持向量机( SVM) 能较好地解决小样本、非线性以及高维数的模式识别问题． 支持向量机通过结构风险最小化原理来提高泛化能力，可以用于解决二元分类问题，已在模式识别、信号处理和函数逼近领域得到应用^［8--9］． 最小二乘支持向量机( least-squares supportvector machine，LS-SVM) 是Suykens 和Vandewalle^［8］在Vapnik 的标准支持向量机的基础上提出的一种改进方法． 最小二乘支持向量机在优化问题中引入误差的平方项，用等式约束取代原先支持向量机的不等式约束条件，将耗时的二次规划问题转化为线性方程组的求解，大幅度地简化了训练过程．

给定具有N 个n 维样本向量的训练集T = { ( x₁，y₁) ，( x₂，y₂) ，…，( x_N，y_N) } ，其中x_k∈Ｒⁿ 是第k 个输入向量，y_k∈Y = { 1，－ 1} 是第k 个输入向量在二元分类问题中的类标签． 当样本在输入空间不能被线性分开时，选择一个非线性映射Φ(·) : Ｒⁿ→H，把样本向量从输入空间Ｒⁿ 映射到特征空间H． 当在特征空间H 构建最优超平面时，训练算法只需要计算该空间向量间的内积，即Φ( x_i) Φ( x_j) ，通过引入核函数κ( x_i，x_j) = Φ( x_i) Φ( x_j) ，使得高维空间的内积运算转化为原始输入空间核函数的计算． 支持向量分类机的目标是在特征空间中构建最优线性决策函数:

其中，Φ(·) 是从输入向量到高维特征空间的非线性映射，ω 是最优分类超平面的法向量，b 为偏移量．

假设训练集在特征空间中是线性可分的，最优分类超平面应满足如下条件:

当训练集在特征空间中为线性不可分时，任何分类超平面都必然有错误的划分，因此不能要求所有训练点均满足约束条件( 2) ． 为此，对第个训练点( x_k，y_k) 引入松弛变量ξ_k≥0，把约束条件放宽为:

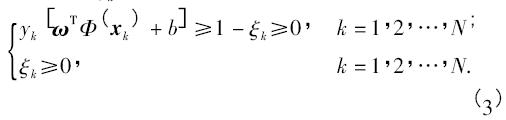
ξ = ( ξ₁，ξ₂，…，ξ_N) 体现了训练集被错分的情况，而由ξ可以构造出表述训练集被错划的程度． 根据结构风险最小化原则，最小二乘支持向量机在目标函数中选取ξ² 作为损失函数，寻找最优超平面的问题转化为下列二次规划问题

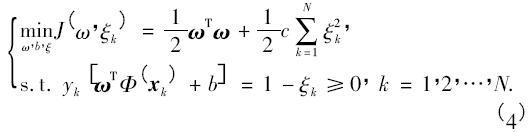
其中，c 是为了均衡目标函数所引进的惩罚系数． 求解式( 4) ，需引入Lagrangian 函数L( ω，b，ξ; α_k) 即

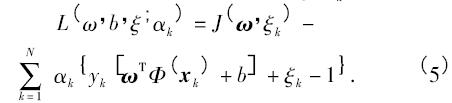
其中α_k为Lagrangian 乘子． 根据Karush--Kuhn--Tucker( KKT) 优化条件^［10］可得

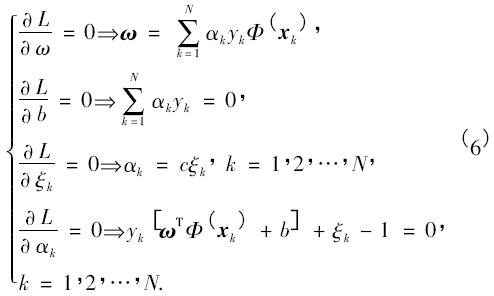
引入某个核函数κ(·) 后，最优化问题最终转化成式( 7) 线性方程组的求解

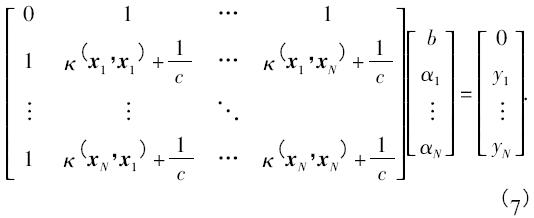
解方程组得到最优解α^* = ( α^*₁，α^*₂，…，α^*_N) 和b^* 得到决策函数

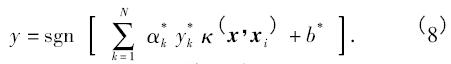
1. 2 Fisher 线性判别纠错输出编码

高炉故障形式多样，不同故障有不同的表现形式．在本文中，我们考虑三种高炉典型故障形式: 悬料、崩料和管道行程，是一种多分类问题． 在实际的应用过程中，支持向量机被证明是强有力的二元分类方法^［11］． 然而，当需要处理多元分类问题时，支持向量机不能直接用来处理这种信息． 在支持向量机算法处理多分类问题中，往往将多元分类问题转化为一对多的二元分类问题． 然而这种转化往往会增加分类器的个数，增加训练时间． 在这一小节中，我们介绍Fisher线性判别纠错输出编码，并将其应用到高炉的多故障识别算法中．

1. 2. 1 纠错输出编码

纠错输出编码( error correcting output codes，ECOC) 是处理多元分类问题的通用框架，它能够通过编码减少数据样本维数，提高样本质量，从而可以保证采用较少的支持向量机分类器建立故障诊断模型，解决支持向量机多元分类问题^［12］． 总体来讲，可以把纠错输出编码方法分解为两个不同的阶段: 编码和解码．在编码阶段，对于一组给定类别的训练样本集合，为每个类别设计一套单独的码字( 代表每个类的编码的比特序列) ，码字的每个位置标示了某一类的训练样本在相应的二元分类器中的标签归属． 在解码阶段，寻找与实验样本分类结果最匹配的码字，指定输入向量的类别标签，从而得到最终的分类决策． 通过拆分重组原始的类别集合并且将二元分类方法嵌入以实际问题为导向的纠错编码设计过程，有效的解决了复杂的多分类问题．

在编码步骤中，对于给定的待学习的N 类样本集合，在为每个类分配一行独一无二的长度为n 的码字时，形成了n 个不同的二元分类问题． 码字的每个比特位根据某类训练样本集在相应二元分类器的归属，被编码为+ 1( 正例) 或者－ 1( 负例) ． 将码字按照矩阵的行向量排列起来，可以得到一个二元的N × n 编码矩阵M，其中M_ij∈{ － 1，+ 1} ． 在此基础上，Allwein等^［13］在编码过程中引入了0 符号，这意味着在某些分类器中某些类的样本是不被考虑的，通过忽略这些类的样本对分类器的影响，三元的纠错输出编码结构丰富了类别划分的多样性，最后得到三元编码矩阵M，其中M_ij∈{ － 1，0，+ 1} ．

在解码步骤中，应用n 个二元分类器，可以得到每个测试样本长度为n 的输出编码，根据输出编码与各个码字之间的距离测度可以决定其类别的归属． 常用的距离测度是汉明距离，对于任意的测试样本的分类结果可以用如下公式表示

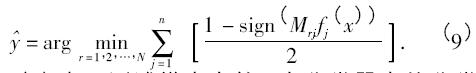
其中，f _j( x) 表示测试样本在第j 个分类器中的分类结果^［14］．

为了寻找码字长度简短并具有高分辨力的编码矩阵，总体的算法描述如下:

第一步，创建列向量编码二叉树，利用以Fisher 线性判别率为标准的浮动搜索法，递归地寻找第k 个父节点的类集合S_k中具有最大判别率的两个分区{ φ¹_k，φ²_k} ．

第二步，根据得到的分割结果{ φ¹_k，φ²_k} 为编码矩阵M 的第k 列赋值．

其中，第一步创建了列向量编码二叉树． 表1 描述了创建列向量编码二叉树的算法． 每一个树节点定义了一个类集合分割的问题，每个节点的分割必须满足使判别率最大化的条件． 通过最大化数据x 和为分割结果所创建的类标签d 之间的交互信息可以得到最终的列代码． 算法中d 是一个离散的随机变量，因此给定类集合S_k的一个分割结果{ φ¹_k，φ²_k} = BP( S_k) ，d按如下形式定义:

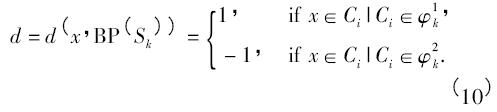
将二叉树视为寻找码字的手段，第二步是填充纠错输出编码矩阵的过程． 利用除了叶节点外的每个根节点得到的列代码，组成了编码矩阵M． 列代码作为矩阵M 的列向量依次排列． 为了创建每一个列代码，可以使用父节点和子节点的关系进行描述． 对于给定的类Cr和节点k 的类集合k: { φ¹_k∪φ²_k} ，其中φ¹_k和φ²_k分别是节点k 的子节点，矩阵M 按如下方式填充:

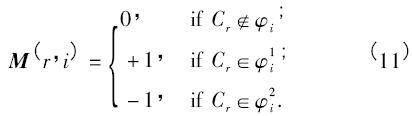
注意到列的数量n 和内部节点的数量一致． 容易得出，在任何的二叉树中，如果叶节点的数量是N_c，内部节点的数量是N_c － 1，因此可以确定码字的长度是N_c － 1．

图 1 展示了一个八元分类问题列向量编码二叉树构造的过程．

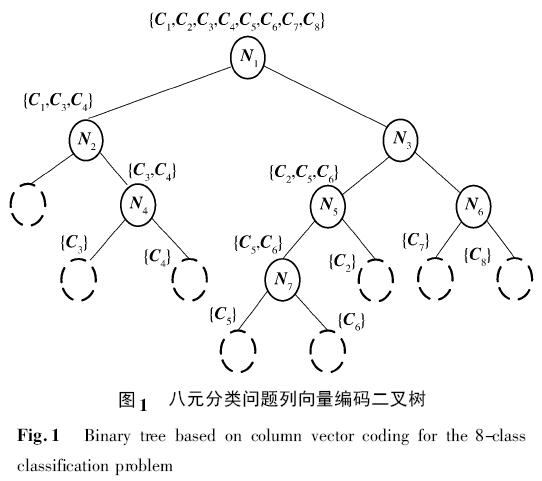
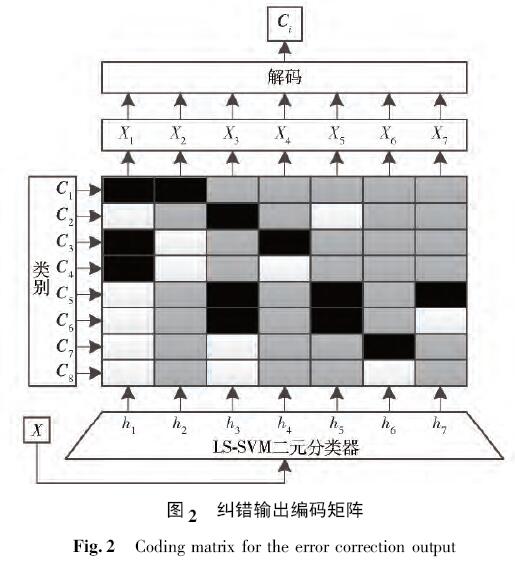
图2 显示了判别纠错输出编码矩阵的结果． 其中白色的方格表示相应的位置被编码为+ 1，黑色的方格表示－ 1，灰色的方格表示0． 因此，C6类的码字是{ 1，0，－ 1，0－ 1，0，1} ． 编码矩阵的第i 列定义了一个二元分类问题，将相应的二元分类器hi进行训练． 例如，分类器h5区分{ C5，C6} 和{ C2} ．

1. 2. 2 Fisher 线性判别浮动搜索法

在本小节，我们设计了一种Fisher 线性判别率为标准的启发式纠错输出编码，并将其运用到判别纠错输出编码算法中． 该算法能够利用较少的支持向量机分类器，实现高炉故障的多分类问题．

回顾表1 中描述的算法，为了将类集合分割成两个部分，需要一个最大化判别率的过程． 但是，最好的分割子集需要在所有可能的分割中无遗漏的寻找，由于这种方法是不切实际的，所以必须使用一种次优的策略． 浮动搜索方法是一种次优的顺序搜索方法，能够缓解穷举搜索法在进行分割选择时，产生的高额计算代价． 而且，这种方法允许搜索方向是变化的，从而解决了许多顺序搜索方法的主要限制．

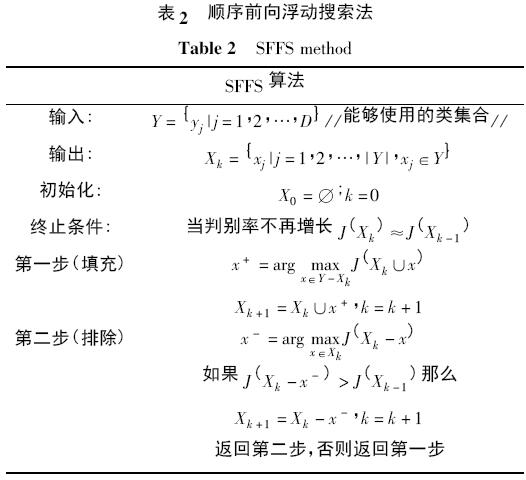
表2 中的方法为顺序前向浮动搜索法( sequentialfloating forward selection，SFFS) ． 这种方法以空的类集合X₀开始并在新集合的判别率增加时被逐渐填充．在填充阶段，对于类集合X_k最有意义的类被纳入进来． 在条件排除步骤，如果判别率继续增长则最差的类被移除．

为了避免高维空间庞大的计算量，选择Fisher 线性判别率作为分割类集合的标准． 假设C₁和C₂是二分类问题的两个类． 定义Fisher 线性判别率为

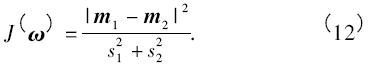
式中m₁和m₂是样本的均值，s₁和s₂是C₁和C₂各自的方差． 定义类内散射矩阵S_ω和类间散射矩阵S_b为:

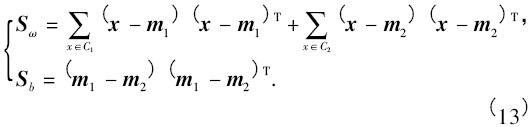
根据上面的结果，J( ω) 可以被写成

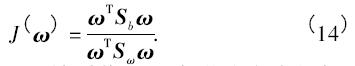
类间散射矩阵S_ω可以被看作是一个类的密度指标．并且，类间散射矩阵S_b可以被看作是一个类的位置指标． 因此，可以定义判别率

1. 3 变尺度离散粒子群

高炉生产环境复杂，生产数据往往遭到工业噪声的干扰，这对于故障识别算法有强鲁棒性的要求． 另外，高炉运行状态繁多，各种炉况之间相互转化，设计稳定可靠的故障分类器至关重要． 最小二乘支持向量机分类算法中学习参数的选择，对于故障分类精度影响严重． 合适的学习参数不仅能够提高分类器的故障识别精度，而且能够保证分类器稳定运行，满足高炉生产的需求． 在此我们采用粒子群算法( particle swarmoptimization，PSO) 对于最小二乘支持向量机分类器的学习参数进行优化． 粒子群算法起源于对鸟群寻找食物行为的模仿［15］． 标准粒子群优化算法主要针对连续参数进行搜索运算，但高炉全局参数优化是离散的组合优化问题，为此需采用离散粒子群优化算法．

假设一个由m 个粒子组成的群体在D 维的搜索空间以一定的速度飞行，粒子i 在第t 次迭代中的状态属性设置如下: x_i = ( x_i1，x_i2，…，x_iD) ，x_id∈［L_d，U_d］为第i 个粒子( i = 1，2，…，m，d = 1，2，…，D) 的维位置矢量，L _d和U_d分别为搜索空间的下限和上限，根据适应度函数计算x_i当前的适应值，即可衡量粒子位置的优劣; v_i = ( v_i1，v_i2，…，v_iD) ，v_id∈［v_min，v_max］为i 粒子的的飞行速度，即粒子移动的距离，v _min和v_max分别为最小和最大速度; p_i = ( p_i1，p_i2，…，p_iD) 为粒子自身迄今为止搜索到的最优位置; p_g = ( p_g1，…，p _gD) 为整个粒子群迄今为止搜索到的最优位置． 对于离散组合优化问题，粒子在每一个维度均被限定为0 或1，更新粒子的位置意味着改变某一位的状态为0 或1，对于速度矢量，其相应位表示的是x_id取0 或1 的概率，在每次迭代中，粒子根据以下等式更新速度和位置:

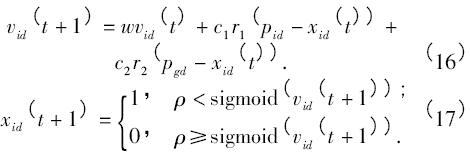
式中: t 是迭代次数; r₁、r₂和ρ 为［0，1］之间的随机数，用于保持群体的多样性; c₁和c₂为学习因子，使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优点以及群体内历史最优点靠近，通常取c₁ = c₂ = 2; w 为惯性权重，其大小决定了粒子对当前速度继承的多少，选择一个合适的w 有助于粒子群算法均衡它的探索能力与开发能力; sigmoid 数是常用的一种模糊函数，其表达式为

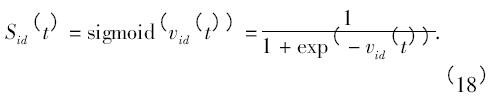
在离散粒子群优化方法( discrete particle swarmoptimization，DSPO) 中，每个粒子平等的更新，忽视了最优粒子的优势． 在现实世界中，大多数社会性动物都存在等级现象，最好的个体往往享受着某些特权．因此根据粒子的表现好坏，应采用不同的进化策略．

首先，运用式( 18) 计算概率向量，即probid = Sid ．然后，根据如下原则更新粒子的概率向量，位置矢量和速度矢量: ( 1) 对于获胜的粒子，根据式( 16) 和式( 17)分别更新其概率向量，位置矢量和速度矢量; ( 2) 对于失败粒子，速度矢量和位置矢量按如下等式更新．

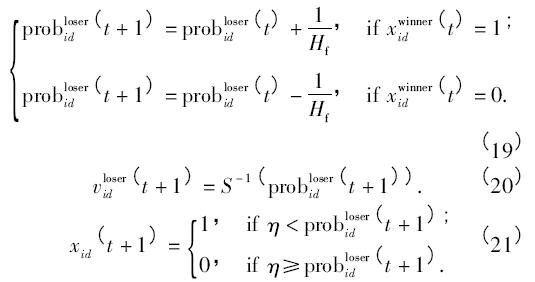
式中，H_f是层次因子，η 为［0，1］之间的随机数．

为了克服粒子过早成熟，在离散粒子群优化方法中引入突变因素． 随着迭代次数增加时，最优的结果没有得到改善，将执行突变操作．

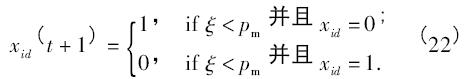
式中，p_m是突变概率，ξ 是［0，1］之间的随机数．

2   高炉智能故障诊断模型

本文依据高炉冶炼原理和在长期生产实践中积累的故障征兆描述，结合宝钢2500 m³高炉自身先进检测技术的优势，对冶炼过程中出现的悬料、崩料和管道行程三种典型故障进行诊断分析．

在进行故障分析时，为了更好地反映真实的炉况状态，不能仅仅依赖高炉现场数据的瞬时值，而是要考虑一段时间内数据的整体特征． 宝钢现场数据采集系统采样间隔为1 s，依据悬料、崩料和管道行程故障出现时在一段时间内产生的异常现象，以900 个采样点为周期，计算数据的均值、方差和变化率，最终确定炉况诊断系统的特征参数向量为F = ( GQ，CQ，HP，TP，ΔP，K) ，其中GQ 为煤气流量，CQ 为冷风流量，HP 为热风压力，TP 为炉顶压力，ΔP 为压差，K 为透气性指数，各参数都由样本均值、方差和变化率组成．

先进的检测技术为故障诊断带来更多的信息支持，宝钢2500 m³高炉在炉顶不同的位置安装有六个微波雷达，用于测量当前料面上六个不同位置的料线深度，雷达数据能够反映径向料面和料速变化的规律．在炉喉斜桥方向开始沿圆周每隔90° 安装一根测温梁，其上共有17 个十字测温点，能自动连续地测出炉喉径向温度，根据温度变化，能判断煤气流在炉喉的径向分布． 在应用改进的均值滤波方法去除六点雷达数据的噪声并采用二维滑动多项式曲面拟合对径向的十字测温数据进行预处理^［16］，最终得到炉况诊断系统的环境信息向量为E = ( Ｒad₁，Ｒad₂，…，Ｒad₆，CT，ＲT，ΔT) ，其中Ｒad_i，i=1，2，…，6 为六点雷达各自的波动值，CT 为中心点温度均值，ＲT 为边沿温度均值，ΔT 为边沿中心温度差． 综合上述参数集，形成最终的高炉诊断输入向量IN = ( F，E) ． 高炉智能故障诊断流程如图3 所示．

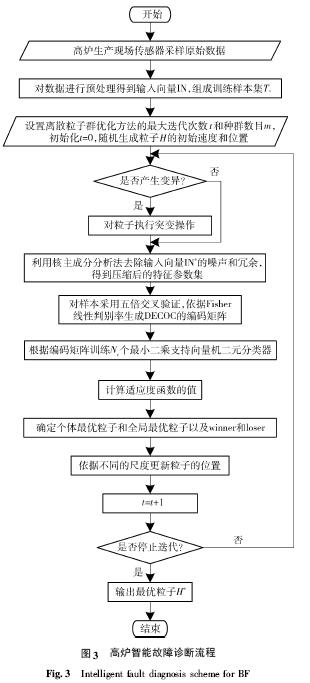
由于生产环境和检测手段的限制，采样数据往往变得极其复杂、混乱和冗余． 未经预处理的采样数据会导致所提取的特征参数受到不同程度的噪声污染，从而影响诊断推理的精度． 由于特征参数选择的随意性且数量众多，构成样本向量的不同特征参数之间常常具有一定的非线性相关性，大量的数据不但占用巨大的存储空间和计算时间，加重了诊断推理机的负担，降低了系统的实时性，而且有用的知识往往会淹没在大量的冗余数据中． 为了分析重要的特征，抑制无用的信息，需要进行特征提取． 本文选用核主元分析法^［17］对数据进行压缩和信息抽取，可以有效地找出数据中最主要的元素和结构，能够消除特征参数间的冗余以及噪声对特征参数的干扰，将原有的复杂数据降维，把众多指标转化为少数几个综合指标，同时保留甚至强化了该数据的主要特征，揭示了隐藏在复杂数据背后的简单结构，从而使数据更容易处理．

在整个诊断系统中，假设c = ( c₁，c₂，…，c _n) 是n 个最小二乘支持向量机二元分类器的惩罚系数，c _i被限定在{ 2⁰，2¹，…，2¹⁰ } ; σ = ( σ₁，σ₂，…，σ_n，σ_KPCA) 是n +1 个径向基核函数的宽度参数，σ_i被限定在{ 2 ^{－ 3}，2^{－ 2}，…，2⁵ } ; f = { f₁，f₂，…，f_m} 是m 个特征参数的特征选择集，f _i = 1 表示第i 个参数被选中，f_i = 0 表示第i 个参数未被选中． 组合上述参数集，形成一个混合向量H= ( c，σ，f) ，需运用变尺度离散粒子群优化方法对其进行优化．

适应度函数是系统总体表现的衡量标准，根据系统的训练准确率、支持向量的数量和参数选择的个数评判每个粒子表现的优劣． 现设定如下形式的适应度函数:

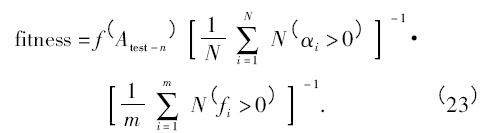
式中，f ( A_{test － n}) 表示对训练集的数据运用n 重交叉检验的平均正确率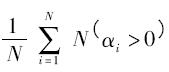，表示支持向量在所有训练样本中占的比例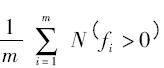，表示选中的特征参数在所有参数中占的比例．

3   实验仿真

为了检验本文提出的基于全局优化支持向量机的多类别故障诊断方法，选取宝钢高炉生产过程中具有代表性的500 组炉况数据，其中正常炉况数据200 组，悬料、崩料和管道行程异常炉况各100 组，利用其中400 组数据作为训练样本，剩余100 组作为测试样本．

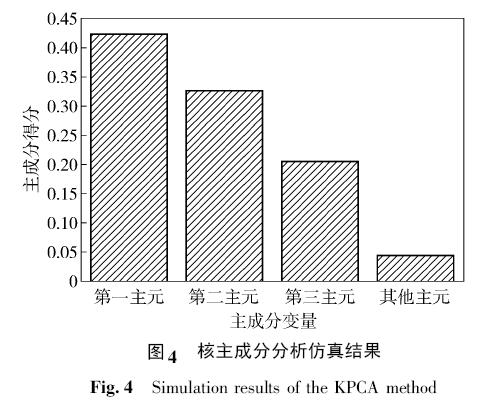
在故障检测模型中，我们提取高炉特征数据IN =( F，E) ． 该特征数据含有15 维特征，采用核主成分分析方法对其进行降维处理． 图4 展示了核主成分分析方法的仿真结果图． 从图中可以看到每个主元所代表数据特征的比重． 我们提取前三个主元所代表的特征数据作为模型的输入． 前三个主元代表了95. 5%的特征属性，能够满足模型的要求．

设置变尺度离散粒子群优化方法最大迭代次数为300 次，最小二乘支持向量机分类器的惩罚因子c =( c₁，c₂，c₃) 和径向基核函数的宽度参数σ = ( σ₁，σ₂，σ₃，σ_KPCA) 的自寻优过程分别如图5 和图6 所示．

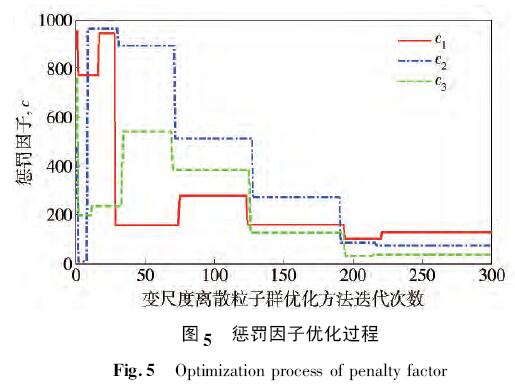
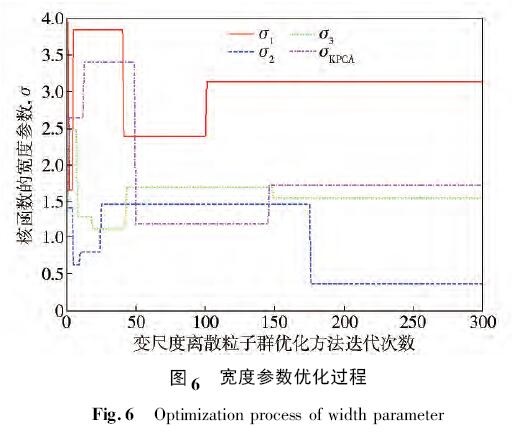
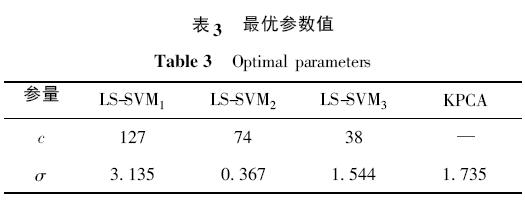
由图5 和图6 可以看出变尺度离散粒子群优化方法在粒子寻优的初期具有极大的搜索范围，粒子的变异性能够有效地防止粒子陷入局部极值，在搜索的后期，该算法能够在小范围内对最优值进行调整，最终得到的最优参数如表3 所示．

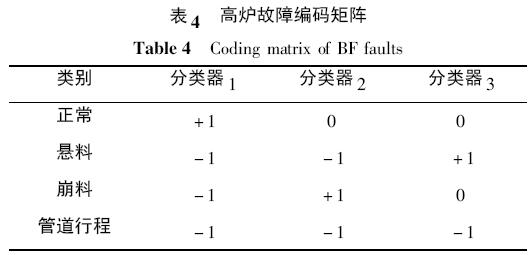
进一步，对高炉故障训练样本采用Fisher 线性判别纠错输出编码法得到编码矩阵，如表4 所示．

在测试阶段，本文将基于参数优化的纠错输出编码多类别故障诊断方法与传统的无参数优化( c = 10，σ = 0. 4) 的一对一、一对多、密集随机编码和稀疏随机编码四种方法进行对比，进行1000 次实验后得到平均结果如表5 所示．

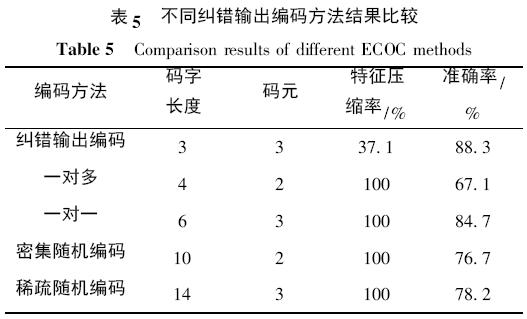
由表5 可以看出故障样本经过特征参数的筛选和压缩之后，显著降低了样本的维数且提高了样本的质量，减轻了最小二乘支持向量机分类器的运算负担，增强了系统的分类性能． 与其他四种方法相比纠错输出编码方法提供了最为紧凑的编码，码字长度代表着采用最小二乘支持向量机分类器的个数． 通过表5 可以看出，通过纠错输出编码后，我们采用三个最小二乘支持向量机的分类器就可以实现高炉故障的识别． 相比于其他算法，分类器的个数得到了很好的抑制，降低了故障识别时间． 利用Fisher 判别率对类集合的重新整合，帮助分类器得到了较高的准确率． 就系统的复杂性而言，一对多方法与纠错输出编码法最为接近，但是前者的准确率却是较低的，因为这种方法容易受到不同类别训练样本数量不均衡的影响． 虽然随机编码方法也得到了可以接受的效果． 但是，由于它们需要构造的分类器数量过多，严重影响了系统的实时性，不利于高炉生产现场炉况的在线监测． 相比而言，一对一方法得到了与纠错输出编码相近的分类结果，并且其编码构造方式固定，构造过程简单，可以作为一种备用的高炉故障诊断系统的编码选择．

4   结论

本文针对特定高炉选取与典型故障密切相关的特征统计参数，从数据预处理和参数优化两个方面着手，应用变尺度离散粒子群优化方法提升了最小二乘支持向量机二元分类器的整体性能，进而通过启发式的纠错输出编码设计，将二元分类器推广至多元故障分类，使用较少的分类器，在提升系统实时性的同时得到了良好的诊断效果，为高炉故障的在线监控提出了一种可行的方法．

参 考 文 献

［1］ Liang J B． The Blast Furnace Condition Diagnosis System Designand Implementation based on the Gas Flow Ｒate ［Dissertation］．Changsha: Central South University，2009

( 梁剑波． 基于煤气流量的高炉炉况诊断系统设计及实现［学位论文］． 长沙: 中南大学，2009)

［2］ Li Q H． Fuzzy Identification Prediction and Control to B． F IronmakingProcess ［Dissertation］． Zhejiang: Zhejiang University，2005

( 李启会． 高炉冶炼过程的模糊辨识、预测与控制［学位论文］． 浙江: 浙江大学，2005)

［3］ Gao C H，Jian L，Chen J M，et al． Data-driven modeling andpredictive algorithm for complex blast furnace ironmaking process．Acta Autom Sin，2009，35( 6) : 725

( 郜传厚，渐令，陈积明，等． 复杂高炉炼铁过程的数据驱动建模及预测算法． 自动化学报，2009，35( 6) : 725)

［4］ Liu L M，Wang A N，Sha M，et al． Fault diagnostics of blast furnacebased on CLS--SVM / / 2010 Chinese Conference on PatternＲecognition． IEEE，2010

［5］ Yang J，Xu Q，Yu C B，et． al． Study on fault diagnosis of blastfurnace based on ICA--QNN / / Proceedings of the 29th ChineseControl Conference． Beijing，2010: 4014

( 杨佳，许强，余成波，等． 基于ICA--QNN 的高炉故障诊断研究/ / 第29 届中国控制会议． 北京，2010: 4014)

［6］ Li Z． Ｒesearch of Blast Furnace Fault Diagnosis based on BayesianNetworks ［Dissertation］． Wuhan: Wuhan University of Scienceand Technology，2015

( 李振． 基于贝叶斯网络( Bayesian Networks) 方法的高炉故障诊断研究［学位论文］． 武汉: 武汉科技大学，2015)

［7］ Pujol O，Ｒadeva P，Vitria J． Discriminant ECOC: a heuristicmethod for application dependent design of error correcting outputcodes． IEEE Trans Pattern Anal Mach Intell，2006，28( 6) : 1007

［8］ Suykens J A K，Vandewalle J． Least squares support vector machineclassifiers． Neural Process Lett，1999，9( 3) : 293

［9］ Xu M，Wang S T，Gu X． TL--SVM: A transfer learning algorithm．Control Decis，2014，29( 1) : 141

( 许敏，王士同，顾鑫． TL--SVM: 一种迁移学习新算法． 控制与决策，2014，29( 1) : 141)

［10］ Gestel T V，Suykens J A K，Lanckriet G，et al． Multiclass LS--SVMs: moderated outputs and coding-decoding schemes． NeuralProcess Lett，2002，15( 1) : 45

［11］ Liu L M，Wang A N，Sha M，et． al． Multi-class classificationmethods of cost-conscious LS--SVM for fault diagnosis of blastfurnace． J Iron Steel Ｒes Int，2011，18( 10) : 17

［12］ Qiu M H，Wang Z Y，An G，et al． Diagnosis of gear fault basedon KPCA and ECOC--SVM． J Vib Shock，2009，28( 5) : 1

( 邱绵浩，王自营，安钢，等． 基于核主元分析与纠错输出编码SVM 的齿轮故障诊断． 振动与冲击，2009，28( 5) : 1)

［13］ Allwein E，Schapire Ｒ，Singer Y． Ｒeducing multiclass to binary:a unifying approach for margin classifiers． Mach Learn Ｒes，2002，12( 1) : 113

［14］ Zhou J D，Wang X D，Cui Y H，et al． Error-correcting outputcodes based on evidence theory for multi-class classification．Control Decis，2013，28( 4) : 495

( 周进登，王晓丹，崔永花，等． 基于证据理论的纠错输出编码解决多类分类问题． 控制与决策，2013，28( 4) : 495)

［15］ Ji Z，Liao H L，Wu Q H． Particle Swarm Optimization Algorithmand Its Application． Beijing: Science Press，2009

( 纪震，廖惠连，吴青华． 粒子群算法及应用． 1 版． 北京:科学出版社，2009)

［16］ Hao Y． Study on Ｒadar and Cross Temperature Data Processingin Blast Furnace ［Dissertation］． Beijing: University of Scienceand Technology Beijing，2012

( 郝宇． 高炉雷达及十字测温数据处理算法研究［学位论文］． 北京: 北京科技大学，2012)

［17］ Cao L J，Chua K S，Chong W K，et al． A comparison of PCA，KPCA and ICA for dimensionality reduction in support vector machine．Neurocomputing，2003，55( 1-2) : 321