周明熙，周昊，马鹏楠，程明

（浙江大学热能工程研究所，能源清洁利用国家重点实验室，浙江 杭州 310027）

摘要：全面了解获取多孔烧结矿的热物理特性对于在钢铁企业中相关过程的运行优化和节能减排具有重要意义。在此前景下，无损的高精度 X 射线显微断层扫描技术被应用到表征烧结矿的孔隙结构并结合数值模拟来预测烧结矿的有效热导率。以 40 µm 的分辨率扫描了 3 个熟石灰添加水平下的烧结杯试验中获取的烧结矿样品。三维重建后的烧结矿可观测到各向异性的非常复杂的孔隙分布，导致其有效热导率也各向差异较大，形成复杂的内部温度场分布。烧结矿中 0～300 µm 的小孔隙在数量频率上占据大多数（约 45%～50%），但仅占小部分的大于 1 mm 的大孔隙则贡献了约 95%的孔隙体积占比，并主要决定了烧结矿的导热行为。3 个烧结矿样品的有效热导率分别为0.645、0.682 和 0.784 W·m ⁻¹ ·K ⁻¹ ，对应的孔隙率分别为 53.8%、53.1%和 49.7%。通过与文献中的类似铁系聚合物的导热值，典型的经验式预测方程和结构分析模型等比较，证明了 CT 三维重建结合数值模拟的技术手段可有效捕捉烧结矿真实的多孔结构，从而比简单的经验式方程或结构分析模型能获取更精确的热物理行为的预测效果。

关键词：X 射线显微断层技术；多孔介质；空隙率；热传导

引 言

在多数钢铁企业中，铁矿石烧结是一个不可或缺的预处理加工过程，以向高炉提供主要的炼铁原料。烧结过程中，各类原料经混匀、制粒后，布料形成透气性合适的颗粒堆积床，在高温作用下物料将部分熔融黏结，最终生产出多孔块状的成品烧结矿。因为固化的熔融相的黏结作用，烧结矿具有由固相物质、颗粒间孔隙及颗粒内孔隙等组成的非常复杂的多孔结构 ^[1-2] 。全面了解获取多孔烧结矿的热物理特性对优化控制相关的工业生产过程具有重要意义，包括有烧结床中的火焰锋面传播 ^[3-5] ，烧结冷却机中的余热回收 ^[6-8] ，以及高炉中的气固两相传热 ^[9-10] 等。

对于精确表征多孔介质的有效热导率，多孔介质的固相物质及孔隙的空间分布不可忽视。传统的基于结构参数获取有效热导率的方法主要可以分为两大类，即试验测量和基于简单几何参数值的经验公式或者分析模型的模拟预测。在试验测量方面，Akiyama 等 ^[11] 采用激光反射法测定了纯铁氧化物及还原的烧结矿的导热率。Sundarmurti 等 ^[12-13] 则通过测量铁矿石球团中心及表面的温度值，再求解径向的热平衡问题的方式获取了球团矿的导热率。Tian等 ^[14] 则考察了采用瞬态平板热源法测定烧结矿有效热导率的可行性。在模拟预测方面，Nishioka 等 ^[15]拍摄了对应多孔烧结矿实际尺寸为 300 µm × 273µm 的显微图片，在该图像上组织了二维的热传递模拟核算出有效热导率。Aizawa 等 ^[16] 则尝试合并了相场法和有限元方法，开发了一种新型的多孔介质的单元格模型以预测烧结矿的有效热导率。此外，一些传统的单元格模型 ^[11] 和分形模型 ^[14] 也曾被提出，这些模型的预测值在前人工作中与其试验测定值均达到了可接受的吻合程度。上述研究中，尽管用于确定多孔烧结矿有效热导率的方法不同，但结论中均指出孔隙的直径、形状、分布等结构特征是影响多孔烧结矿的热学特性和传热表现的重要因素。

近年来，数值模拟技术与 X 射线显微扫描技术均取得了显著发展，已可实现在较快的计算速度和较高的分辨率的条件下进行三维真实多孔结构下的数值模拟 ^[17] 。通过结合 CT 三维重建和数值模拟以预测多孔介质的有效热导率的研究已被大量报道，这些多孔介质包括金属泡沫 ^[18-19] ，天然气水合物沉积物 ^[20] 和绝缘混凝土 ^[21] 等。然而，以此种方法对多孔烧结矿进行有效热导率的预测仍未见报道。尽管CT 扫描技术在 20 世纪 90 年代便被日本的学者引入到铁矿石烧结过程的研究中，但大多数前人的研究仅关注于孔隙结构的评估及其对烧结床层透气性 ^[22-25] 和烧结矿的冶金性能的影响 ^[26] 。

本文基于高分辨率的X射线显微断层扫描的结果，对 3 个不同熟石灰水平下的烧结矿的孔隙结构特征进行了量化评估。结合三维重建的真实多孔结构，以有限元方法进行数值模拟预测了这些烧结矿的有效热导率，并与已有文献中的试验值、经验公式、分析模型等进行了比对验证。最后，对烧结矿的孔隙特征与有效热导率间的关系进行了细致的讨论及阐述。

1 试验方法

1.1 X 射线显微断层扫描

用于X射线显微断层扫描的烧结矿来源于中试规模的烧结杯试验台。该烧结杯内径 300 mm，高600 mm，每次试验均按照标准操作流程进行 ^[27-28] 。熟石灰在现场生产中常作为粘合剂添加至制粒过程中，能有效提高床层透气性及烧结矿产率。烧结杯试验条件如表 1 所示，本文测试的 3 个烧结矿样品对应于 3 个熟石灰添加水平，分别为 0、1%和 2%。烧结杯试验完成后，将整体的烧结块从烧结杯中倒出，然后从床层中部挖取烧结矿样品供后续的 CT扫描检测。

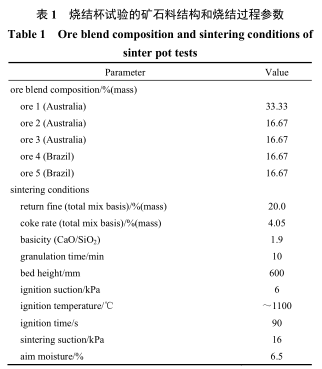
图 1 为进行微米级 X 射线显微扫描检测的系统，烧结矿样品的扫描设置参数见表 2。因 X 射线显微扫描检测的技术原理及仪器条件限定，样品扫描的分辨率一般为样品尺寸的千分之一。原则上说，样品的扫描分辨率越高，孔隙特征的统计及有效热导率的预测将更加准确，但过高的分辨率将导致样品尺寸过小样品代表性降低，后续数值模拟的计算成本也太过巨大而难以进行。考虑到钢铁企业的实际生产中，一般 5～40 mm 的烧结矿将作为成品输送至高炉中作为炼铁原料，参考文献[26]中的设定值，本文针对烧结矿导热研究选取的样品尺寸为 35mm×35 mm×35 mm 左右，分辨率确定为 40 µm。此样品尺寸和分辨率条件下可基本捕捉到烧结矿中大多数的孔隙，且能匹配好 CT 扫描系统的硬件条件及后续数值模拟的计算成本。

1.2 CT 图像处理分析

为分析烧结矿的孔隙结构，对 CT 扫描所获取的切片图像的处理分析过程介绍如下。图 2 (a) 所示为典型的 8 位 CT 切片的灰度图，固相物质相比于空气具有更高的密度，在扫描过程中将吸收更多的 X 射线，在灰度图中表现出更大的灰度值。首先，从原始的灰度图中截取出一个25 mm×25 mm的兴趣域，如图 2 (b) 所示。然后，选取典型的灰度阈值以区分出孔隙和固相物质，对该兴趣域图片进行二值化。孔隙部分灰度值全部设置为 0[图 2 (c) 中的浅色区域]，而固相物质部分灰度值全部设置为255[图 2(c) 中的深色区域]。最后，对二值化后的图片进行三维分水岭算法演算，以分离出各孔隙从而可对孔隙的体积、当量球形直径和球形度等形态学参数进行量化统计。

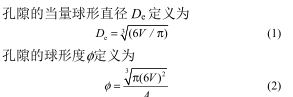
式中，V 为孔隙部分的体积，m³ ；A 为孔隙部分的面积，m² 。

1.3 有效热导率的模拟预测

为计算烧结矿的有效热导率 k e ，采用有限元方法对 25 mm×25 mm×25 mm 的兴趣域进行数值模拟。该立方块计算域采用结构化六面体网格进行划分，模拟的边界条件设置如图 3 所示 ^[18-19] 。某一方向上的对立面间的温差ΔT 设置为 100 K（入口面温度为 573 K，出口面温度为 473 K），其余周界的 4 个面均设置为绝热面。固相物质部分假想为均质，其热导率 k s 为 2.881 W·m⁻¹·K⁻¹，与 Tian等 ^[14] 的分形模型中所使用的数值相同。假设孔隙中的空气(k a =0.023 W·m⁻¹·K⁻¹)为处于静态并无压力梯度从而仅需对该立方块计算域求解能量方程。该模拟在配有 Intel Xeon E5-2683 ×2 CPU (2.0GHz)和 128 GB RAM 的工作站上进行，当相关变量的残差小于 1.0×10⁻⁵时认为模拟达到收敛，每个工况所需模拟时间为 4～6 h。烧结矿的有效热导率计算如下

2 结果与分析

2.1 烧结矿孔隙特征

各烧结矿的固相物质部分的三维重建结果如图4 左列所示。Shatokha 等 ^[26] 定义了接触到兴趣域边界的孔隙为开孔而未接触到兴趣域边界的孔隙为烧结矿内部的闭孔，从而分别讨论了开孔与闭孔的分布情况。依据此逻辑，移除接触边界的开孔后，剩余的闭孔部分则展示在图 4 的右列。从图 4 中可见，因为烧结矿是由堆积床中的颗粒部分熔融黏结而成，烧结矿固相物质本身很不规则，孔隙也极具随机性，其分布极其复杂。烧结矿的孔隙率 ε 计算如下

式中， V_s 为固相物质部分所占空间，m³ ； V_d 为25 mm×25 mm×25 mm 立方块兴趣域的体积，m³ 。

3 个熟石灰添加水平下的烧结矿的孔隙率分别为 53.8%、53.1%和 49.7%。需要指出的是，文献中已报道的烧结矿的孔隙率数值差别很大，与烧结矿的生产条件和使用的检测方法紧密相关。Higuchi等 ^[2] 开发了一种孔包裹（PAC）方法测定出烧结矿的孔隙率在 42.2%～54.5%。Tian 等 ^[14] 则仅测定出烧结矿的内部闭孔，报道的闭孔孔隙率在 12.1%～23.8%。一般而言，采用压汞方法测定孔隙，其测量的量程范围有限，测定的孔隙率结果会普遍偏低。

例如，Bhagat 等 ^[29] 采用压汞仪仅测定了 0.03～58µm 的孔隙，得到的孔隙率为 7.4%～13.4%。相比于上述测量方法，三维 CT 扫描技术具有更宽的孔隙量程范围、相对高的分辨率等优点，且可区分统计开孔和闭孔情况。Shatokha 等 ^[26] 采用三维 X 射线显微扫描技术对 9～25 mm 的烧结矿样品进行了分辨率为 20 µm 的测试，报道了开孔部分的孔隙率在5.3%～43.6%而闭孔部分的孔隙率在 3.1%～7.6%。Zhou 等 ^[30-31] 采用小型制粒转鼓试验研究了熟石灰添加水平对制粒后颗粒堆积成的生料烧结床的孔隙率。依据他们的试验结果，在 6.5%水分条件下，将熟石灰水平从 0 增加至 2%，可使生料床层孔隙率从 38.0%提高至 40.0%。然而，3 个成品烧结矿样品的孔隙率随熟石灰水平的增加反而呈递减趋势。

造成生料床孔隙率与烧结矿孔隙率的变化趋势差异的原因可能是增加熟石灰能促进高温过程中生成的熔融液相的流动，使颗粒合并凝结得更为充分。

将兴趣域中的孔隙按其当量球形直径的大小划分为多组，各组孔隙的数目频率分布如图 5 所示。对扫描的 3 个烧结矿样品，0～300 µm 的孔隙均占到总孔隙数目的 45%～50%，这些微米级的小孔隙主要对烧结矿的 RDI 和 RI 等冶金性能具有显著影响 ^[2,26,29,32] 。Shatokha 等 ^[26] 检测的烧结矿的孔隙尺寸的分布峰值约为 200 µm。需指出的是，本文中采取的扫描分辨率为 40 µm，有部分当量球形直径为80～120 µm（2～3 个像素）的孔隙可能在去噪及分水岭算法中被移除，导致 0～120 µm 部分的孔隙数目被低估。因此，本文的孔隙尺寸的分布峰值略高于 Shatokha 等 ^[26] 报道的结果。

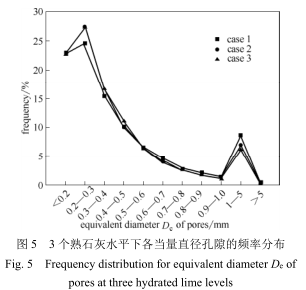
图 6 为3 个熟石灰水平下的各组孔隙的球形度。随着孔隙当量球形直径的增加，孔隙的球形度逐渐降低，0～200 µm 组的孔隙球形度为 0.31 左右，大于 5 mm 组的孔隙球形度仅为 0.19 左右。烧结过程中，在温度高于 1100℃的火焰前锋中会发生固相-熔融相-孔隙的合并，此合并过程仅维持 2～4 min。固相-熔融相-孔隙的三相混合物在合并过程中会重新塑形以降低表面积来达到低能量状态 ^[3] 。因为可流动的熔融液相的表面张力与孔隙直径呈反比，小直径的孔隙将更易成圆形更显规则。测试的 3 个工况中，随着熟石灰添加比例的增加，相同尺寸的孔隙的球形度逐渐增加。出现这种现象的原因可能是，随着熟石灰添加比例的增加，制粒后的颗粒具有更厚的黏附层，从而在火焰前锋中可形成较多的低黏度的熔融液相，孔隙合并发展得更为充分 ^[1,30] 。

图 7 为 0～1 mm、1～5 mm、5 mm 以上的各组孔隙对总孔隙体积的贡献占比。对于扫描的 3 个烧结矿，大于 1 mm 的孔隙对其总孔隙体积的贡献占比分别为 96.24%、96.51%和 95.07%。这与 Kasama等 ^[22] 的结论相一致，孔隙尺寸存在着典型的分界线从而可区分出不同组孔隙的主要作用。尽管 0～1mm 的孔隙在数量频率上占大多数，但它们对总孔隙体积的贡献占比非常小以至于可忽略不计。因此，烧结矿的热物理特征应主要与宏观的毫米级孔隙相关而与微观的微米级孔隙相关度不大。在去噪及分水岭算法中，即便部分 0～120 µm 的孔隙数目被低估，因为该部分微细孔隙对总孔隙体积贡献更可忽略不计，这对后续数值模拟预测的有效热导率的精度将基本无影响。

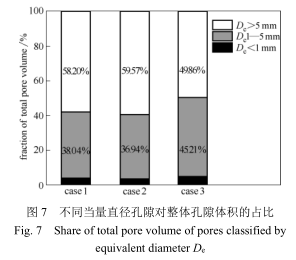
2.2 烧结矿有效热导率

表 3 列出了 3 个烧结矿各空间方向上的有效热导率的数值模拟结果。同一烧结矿的各向有效热导率有一定差别，与烧结矿的多孔结构分布紧密相关，联立图 4 可见，尤其与连通的作为气流通道的大孔隙的空间分布相关。图 8 展示了模拟 3 个烧结矿 x轴方向的有效热导率时的 xy 和 xz 两个平面的温度云图，可明显见到热波在导热性更强的固相中传播得更为迅速。温度场的复杂分布也再次呈现了多孔结构对热物理特性的本质影响，case 1 的具有最大孔隙度的烧结矿中的温度场分布更为均匀。

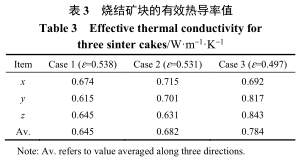
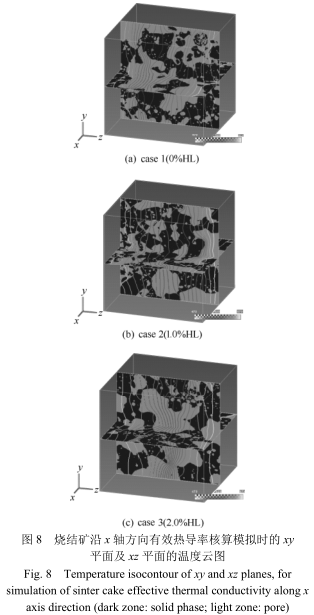
图 9 中对比展示了本文 CT 三维重建模拟预测出的有效热导率与文献中的类似铁系聚合物的报道值。随着烧结矿孔隙率的增大，具有更强导热性的固相物质逐渐减少，有效热导率呈降低趋势。Tian等 ^[14] 的工作中测试的烧结矿颗粒可能是与本文的烧结矿样品最为相近的铁系聚合物。然而，他们仅测量了烧结矿的闭孔，得到的孔隙率为 12.1%～23.8%，对应的有效热导率为2.15～1.27 W·m⁻¹·K⁻¹。

本文中采用 CT 三维重建的模拟方法，包含了更多的大尺寸的开孔，因此样品的孔隙率大至 49.3%～53.8%，有效热导率为 0.615～0.843 W·m⁻¹·K⁻¹。对于 Sundarmurti 等 ^[12-13] 的工作中报道的有效导热值，他们测定的样品为压缩的铁矿石球团，在相同的孔隙率条件下将具有更大的接触界面面积，意味着在固体物质和孔隙的交界面具有更大的热阻。另外，球团矿可能因其碱度较低，其内部矿物成分与烧结矿也差异较大。因此，这些球团矿在 24.1%～38.6%的孔隙率间的有效导热率为0.766～1.200 W·ms⁻¹·K⁻¹，产生了相比于本文的烧结矿它们在更低的孔隙率区间却具有相近的有效热导率的混淆现象。

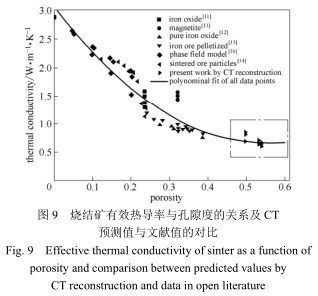
前人研究提出了多种经验式方程和结构分析模型以预测多孔介质的有效热导率 ^[33] 。表 4 中列出了 8 个典型的经验式方程。其中，式（5）和式（6）分别为假想所有孔隙的方向为平行和垂直于热流方向情况下获得的有效热导率。式（7）和式（8）分别是 Maxwell-Eucken 模型的上限值和下限值的表达式，假想多孔介质中具有随机分布的小球孔隙。式（9）为基于相互性理论的相互性模型，假想两相的微观结构在两相的体积比对换时仍将在统计意义上保持平衡 [34] 。式（10）、式（11）和式（12）是组合了平行孔隙和垂直孔隙的经验公式，该公式依据于金属泡沫的大量试验值确定其经验参数，对金属泡沫的有效热导率的预测效果良好 ^[35-36] 。式（13）是 Kaviany 等 ^[37] 开发的针对于球形颗粒的多孔堆积床的经验公式。上述经验式方程随孔隙率变化的计算结果均展示在图 10 中，并与本文的热导率结果和文献值进行了对比。可见，这些简单的经验式方程并不能在较宽泛的孔隙度范围内（10%～60%）对烧结矿的有效热导率取得较好的预测效果。

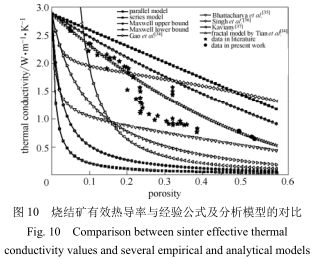
除表 4 中的经验式方程外，基于统计学自相似性的分形模型也表示在图 10 中。分形模型中输入的分形维数参数同 Tian 等 ^[14] 的工作中保持一致，包括分割尺寸 C =7，恒定边长 L =13，迭代阶段 N 和量纲 1 的接触热阻 t + 等。由图 10 可见，相比于所述的经验式方程，此分形模型在较宽泛的孔隙度范围内预测的热导率与文献报道的热导率匹配效果较好。

本文采用 CT 三维重建结合数值模拟预测的各烧结矿的 3 个空间方向的有效热导率平均值与该分形模型吻合良好，表明自相似性可以在一定程度上代表空间全局的孔隙结构特征。然而，CT 重建结合数值模拟的技术能更为精确地捕捉到固相与气相物质沿不同空间方向的分布对导热情况的影响，例如在表 3 中，case 3 烧结矿样品沿 x 轴方向的有效热导率为 0.692 W·m⁻¹·K⁻¹，而沿 z 轴方向为 0.843W·m−1·K⁻¹，区分度明显，在需要高精度的情况下将是最优选择。在考虑低成本的情境下则可采用分形模型进行有效热导率的粗略预测。

3 结 论

本文的研究验证了无损的X射线显微扫描技术对于重建烧结矿的多孔结构并基于真实结构进行数值模拟预测其有效热导率的可行性。对 3 个熟石灰添加水平下的烧结杯试验中取样的烧结矿进行了CT 扫描分析和数值模拟。考虑到设备条件及数值模拟计算的成本等，本文的样品尺寸和分辨率分别确定为 35 mm×35 mm×35 mm 和 40 µm。主要的结论总结如下。

（1）3 个烧结矿的孔隙率分别为 53.8%、53.1%和 49.7%，烧结矿的孔隙率随熟石灰的添加比例呈递减趋势。烧结矿的孔隙结构非常复杂，各向异性且随机分布，同时包含有开孔和闭孔。通过 CT 图像处理分析，统计获得了不同当量球形直径的各组孔隙的数目频率分布及球形度。0～300 µm 的小孔隙在频率分布上占 45%～50%，但其对总孔隙体积的贡献比可忽略不计。大于 1 mm 的大孔隙则贡献了约 95%的总孔隙体积。因此，微米级的小孔隙主要影响烧结矿的冶金性能，而烧结矿的热物理特性则主要受毫米级的大孔隙影响，尤其是大于 5 mm的连通性的大孔隙通道。

（2）结合 CT 三维重建和数值模拟以预测烧结矿的有效热导率是切实可行的。烧结矿的有效热导率随着其孔隙率的增加逐渐降低。烧结矿内的温度场分布也明显各向异性，孔隙度更大的烧结矿内的温度场分布更为均匀。需指出的是，本文 3 个烧结矿样品的孔隙度的区分度相对较小，在后续研究中，可深入考察影响烧结热转换过程中熔融量形成的主要因素，包括焦炭配比、碱度水平等，以获取孔隙率区分度更大的样品，从而可更为了解烧结过程中孔隙结构的演变规律及其导热情况。在预测多孔介质有效热导率的经验式方程和结构分析模型中，基于自相似性的分形模型能与文献中的大多数热导率和本文的预测结果吻合良好，但分形模型并不能捕捉到三维空间方向的细节差异。CT 三维重建结合数值模拟的技术具有获取真实多孔结构的显著优点，在需要高精度预测结果的情况下推荐使用。

References

[1]  DEBRINCAT D, LOO C E, HUTCHENS M F. Effect of iron ore particle assimilation on sinter structure[J]. ISIJ Int., 2004,  44 :1308-1317.

[2]  HIGUCHI K, NAITO M, NAKANO M, et al. Optimization of chemical composition and microstructure of iron ore sinter for low-temperature drip of molten iron with high permeability[J]. ISIJ Int., 2004,  44 : 2057-2066.

[3]  LOO C E, HEIKKINEN J. Structural transformation of beds during iron ore sintering[J]. ISIJ Int., 2012,  52 : 2158-2167.

[4]  LOO C E, ELLIS B G. Changing bed bulk density and other process conditions during iron ore sintering[J]. ISIJ Int., 2014,  54 : 19-28.

[5]  ZHOU H, ZHOU M X, LIU Z H, et al. Factors controlling high-temperature zone resistance to airflow during iron ore sintering[J]. ISIJ Int., 2015,  55 : 2556-2565.

[6]  LIU Y, YANG J, WANG J, et al. Energy and exergy analysis for waste heat cascade utilization in sinter cooling bed[J]. Energy, 2014,67 : 370-380.

[7]  ZHANG X H, CHEN Z, ZHANG J Y, et al. Simulation and optimization of waste heat recovery in sinter cooling process[J]. Appl.Therm. Eng., 2013,  54 : 7-15.

[8]  YANG J Y, CHIU Y W. 3-D transient conjugated heat transfer and fluid flow analysis for the cooling process of sintered bed[J]. Appl.Therm. Eng., 2009,  29 : 2895-2903.

[9]  NATSUI S, TAKAI H, NASHIMOTO R, et al. Model study of the effect of particles structure on the heat and mass transfer through the packed bed in ironmaking blast furnace[J]. Int. J. Heat Mass Transfer,2015,  91 : 1176-1186.

[10] FU D, CHEN Y, ZHAO Y F, et al. CFD modeling of multiphase reacting flow in blast furnace shaft with layered burden[J]. Appl.Therm. Eng., 2014,  66 : 298-308.

[11]  AKIYAMA T, OHTA H, TAKAHASHI R, et al. Measurement and modeling of thermal conductivity for dense iron oxide and porous iron ore agglomerates in stepwise reduction[J]. ISIJ Int., 1992,  32 :829-837.

[12] SUNDARMURTI N S, RAO V. Effect of firing temperature and porosity on thermal conductivity and diffusivity of iron ore pellets[J].ISIJ Int., 1996,  36 : 991-999.

[13] SUNDARMURTI N S, RAO V. Thermal conductivity and diffusivity of iron ore pellet having low porosity[J]. ISIJ Int., 2002,  42 : 800-802.

[14] TIAN F Y, HUANG L F, FAN L W, et al. A comprehensive characterization on the structural and thermophysical properties of sintered ore particles toward waste heat recovery applications[J]. Appl.Therm. Eng., 2015,  90 : 1007-1014.

[15] NISHIOKA K, MURAYAMA T, ONO Y. Estimation of effective thermal diffusivity of porous solid using data for image processing[J].ISIJ Int., 1996,  36 : 150-155.

[16] AIZAWA T, SUWA Y. Meso-porous modeling for theoretical analysis of sinter ores by the phase-field, unit-cell method[J]. ISIJ Int., 2005,45 : 587-593.

[17] MAIRE E, WITHERS P J. Quantitative X-ray tomography[J]. Int. Mater. Reviews, 2016,  59 : 1-44.

[18] ZAFARI  M,  PANJEPOUR  M,  EMAMI  M  D.Microtomography-based numerical simulation of fluid flow and heat transfer in open cell metal foams[J]. Appl. Therm. Eng., 2015,  80 :347-354.

[19] RANUT  P,  NOBILE  E,  MANCINI  L.  High  resolution microtomography-based CFD simulation of flow and heat transfer in aluminum metal foams[J]. Appl. Therm. Eng., 2014,  69 : 230-240.

[20] YANG L, ZHAO J F, LIU W G, et al. Experimental study on the effective thermal conductivity on hydrate-bearing sediments[J].Energy, 2015,  79 : 203-211.

[21] CHUNG S Y, HAN T S, KIM S Y, et al. Evaluation of effect of glass beads on thermal conductivity of insulating concrete using micro CT images and probability functions[J]. Cem. Concr. Compos., 2016,  65 :150-162.

[22] KASAMA S, INAZUMI T, NAKAYASU T. New analysis method of sinter cake pore structure for permeability evaluation[J]. ISIJ Int.,1994,  34 : 562-569.

[23] NAKANO M, KAWAGUCHI T, KASAMA S, et al. Analysis of three dimensional structure of iron-ore sintercake[J]. ISIJ Int., 1997,  37 :339-344.

[24] NUSHIRO K, OYAMA N, IGAWA K, et al. Analysis of flow behavior of fluid during sintering process with large amount of pisolitic ore by hot stage X-ray CT scanner[J]. Tetsu Hagane J. ISIJ,1997,  83 : 472-478.

[25] NAKANO M, KASAMA S, HOSOTANI Y. Effects of limestone size on pore structure of sintercake of iron ore[J]. Tetsu Hagane J. ISIJ,1999,  85 : 711-716.

[26] SHATOKHA V, KOROBEYNIKOV I, MAIRE E, et al. Iron ore sinter porosity characterisation with application of 3D X-ray tomography[J]. Ironmak. Steelmak., 2010,  37 : 313-319.

[27] ZHOU H, ZHOU M X, LIU Z H, et al. Modeling NO x emissions of coke combustion in iron ore sintering process and its experimental validation[J]. Fuel, 2016,  179 : 922-931.

[28] ZHOU H, ZHOU M X, CHENG M, et al. Experimental study and X-ray  microtomography  based  CFD  simulation  for  the characterization of pressure drop in sinter bed[J]. Appl. Therm. Eng.,2017,  112 : 811-819.

[29] BHAGAT R P, CHATTORAJ U S, SIL S K. Porosity of sinter and its relation with the sintering indices[J]. ISIJ Int., 2006,  46 : 1728-1730.

[30] ZHOU H, ZHOU M X, O’DEA D P, et al. Influence of binder dosage on granule structure and packed bed properties in iron ore sintering process[J]. ISIJ Int., 2016,  56 : 1920-1928.

[31] ZHOU M X, ZHOU H, O’DEA D P, et al. Characterization of granule structure and packed bed properties of iron ore sinter feeds that contain concentrate[J]. ISIJ Int., 2016,  57 : 1004-1011.

[32] HOSOTANI Y, KONNO N, YAMAGUCHI K, et al. Reduction properties of sinter with fine dispersed pores at high temperatures of 1273 K and above[J]. ISIJ Int., 1996,  36 : 1439-1447.

[33] WANG M, PAN N. Predictions of effective physical properties of complex multiphase materials[J]. Mater. Sci. Eng. R-Rep., 2008,  63 :1-30.

[34] GAO L, GU J Z. Effective dielectric constant of a two-component material with shape distribution[J]. J. Phys. D: Appl. Phys., 2002,  35 :267-271.

[35] BHATTACHARYA A, CALMIDI V, MAHAJAN R. Thermophysical properties of high porosity metal foams[J]. Int. J. Heat Mass Tran.,2002,  45 : 1017-1031.

[36] SINGH R, KASANA H. Computational aspects of effective thermal conductivity of highly porous metal foams[J]. Appl. Therm. Eng.,2004,  24 : 1841-1849.

[37] KAVIANY M. Principles of Heat Transfer in Porous Media[M]. 2^nd ed. New York: Springer, 1999.