郑朋超1，陈辉2，陈艳波1，武建龙2，王伟2

( 1． 首钢京唐钢铁联合有限责任公司炼铁部，河北唐山063200; 2． 首钢技术研究院钢铁研究所，北京100043)

摘要: 根据炉料在旋转溜槽运动过程的实际情况，建立了相应的运动方程和数学模型，重点研究了科氏力对料流轨迹的影响。模拟研究结果显示: 受科氏力的作用，炉料在溜槽出口处的速度降低，且溜槽总长度越长，布料倾角越大时的作用效果更加显著; 科氏力的作用，使溜槽内的炉料发生偏转升高，对主料流轨迹和落点位置产生影响，在溜槽转速越快时，作用的效果越大。

关键词: 高炉; 布料溜槽; 科氏力

0 引言

目前大型高炉基本上都采用溜槽布料，炉料在加入高炉的过程中大致要经过中心喉管垂直下降，沿旋转溜槽滑落，在“空区”中类似抛物线降落3 个阶段，3个运动阶段的变化均会对炉料的运动轨迹产生影响，进而影响到炉料的落点位置。然而，已有布料模拟大多为静态模型条件下完成的，对炉料在布料溜槽和炉内“空区”的受力和运动考虑不足。

尤其是科氏力对布料的影响较为重要。在地球北( 南) 半球，物体沿经线运动时，受到向右( 左) 的科里奥利力作用，使运动方向不断向右( 左) 偏侈，这一现象称科氏力定律。1835 年，由法国工程师和数学家G． Coriolis 首先确定，科氏力存在于坐标架旋转的参考系内运动的质点。炉料在无钟布料溜槽旋转过程中滑落即受到科氏力的作用，炉料受到的科氏力如式1 所示。

F_c = 2 mυ × ω ( 1)

式中，F_c ———科氏力，N;

m ———质点的质量，kg;

υ ———质点的运动速度，m /s;

ω ———旋转角速度， rad /s。

国内学者对溜槽布料过程中炉料受科氏力影响的情况进行过研究。陈令坤等研究认为^［1］: 炉料颗粒在溜槽上运动时会受到许多力的作用，由炉料质点在溜槽上的受力分析可知，炉料沿溜槽向下滑动的速度可分解为沿溜槽长度方向和底面切线方向的分量。滕召杰等通过研究认为^［2］: 炉料颗粒进入旋转溜槽后，继续运动，颗粒在旋转溜槽内所受的力包括重力、离心力、支持力、摩擦力、科氏力。综合分析颗粒所受力，可以得出颗粒在溜槽内的运动并非一维的直线运动，而是沿着溜槽内壁做螺旋运动; 对于无钟炉顶高炉，旋转溜槽是其中的核心设备，炉料从料罐流出落至溜槽上后受到溜槽的控制作用，溜槽按指定程序旋转及倾动可将炉料合理分布至炉喉料面上。实验及生产实践均表明，炉料落至溜槽后不仅沿其轴向向下运动，同时也在溜槽横截面上发生偏转运动，故可将颗粒在溜槽内的复合运动分解为轴向运动和切向运动^［3］。

本文主要研究了在高炉布料过程中科氏力及溜槽相关参数对焦炭出口速度及落点的影响。

1 模型的建立

1． 1 炉料的受力分析

假定炉料以υ₁速度，自中心喉管垂直下落至溜槽，由于炉料受到溜槽底面强烈的冲击作用，其运动速度和方向都会发生改变，使炉料沿溜槽长度方向的初始运动速度υ₂发生变化，如式( 2) 所示。

υ₂ = K × υ₁ cos α ( 2)

式中，K———速度衰减系数，－ ;

α ———溜槽倾角，°。

旋转溜槽上滑落的炉料受力状态如图1 所示。

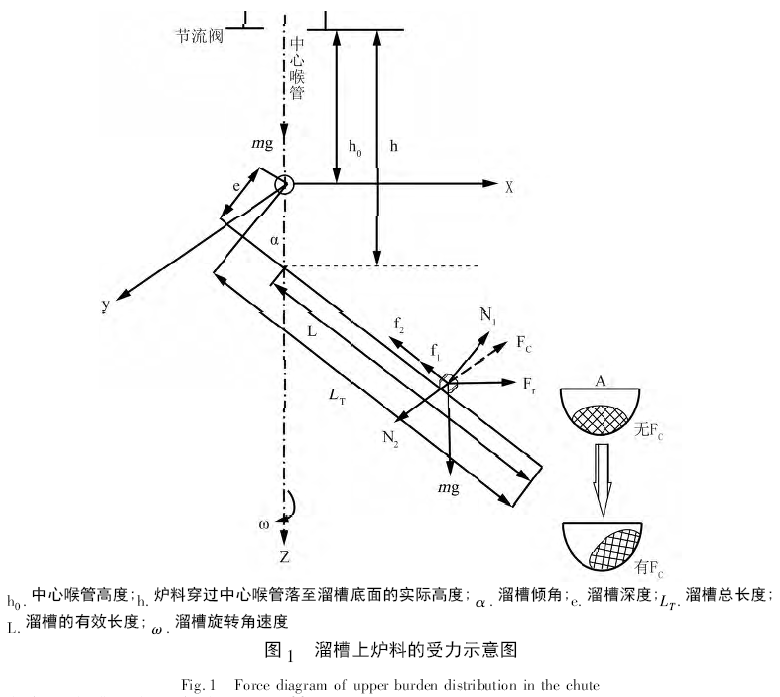
炉料质点在沿溜槽滑落过程中的受力情况: mg为垂直向下的重力，垂直于溜槽底面的正压力N1，与溜槽侧面垂直的侧压力N2，如式( 3) 所示。f1和f2为与运动方向相反的摩擦力，Fc为科氏力、其与N2大小相同、方向相反，F r为离心力。炉料若不受科氏力的作用，其在溜槽内的断面形状近似椭圆状如图1 中( A) 所示; 但由于受到科氏力的作用，其在溜槽内的断面形状发生变化，如图1 中( B) 所示，炉料偏向溜槽一侧并沿溜槽向下滑落。

N₂ = 4 m π ω × υ sin α ( 3)

1． 2 炉料的运动模型

基于上述炉料在溜槽上的受力分析，根据牛顿第二定律可知，炉料在溜槽上的运动模型如式( 4)所示。

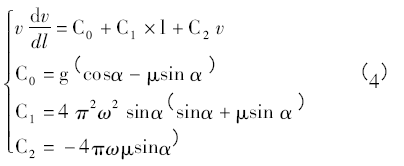
其中C₀、C₁、C₂为常数; 若不考虑科氏力，炉料在溜槽上的运动为式( 4) 中C₂ = 0 时的特殊情形。

式( 4) 所示炉料在溜槽上的运动模型的求解可采用经典Ｒunge － Kutta 四阶方法，通过编制相关计算机程序解出，并能方便地得到炉料在离开溜槽末端时的速度υ₃ 。炉料离开溜槽的速度υ₃可分解为x 、y和z 3 个方向的分速度，如式( 5) 所示。

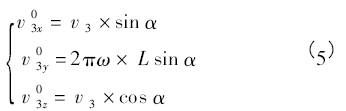
2 科氏力影响炉料运动轨迹的解析结果

2． 1 相关参数的确定

基于前文已建立的炉料在溜槽上的运动模型，可得到炉料沿溜槽向下滑落的过程中，不同溜槽位置的运动速度，其中炉料离开溜槽时的速度即是炉料进入空区，并在空区运动的起始速度，而炉料在空区的运动轨迹前人已做过大量的研究^{［4 － 6］}。受科氏力的影响，炉料离开溜槽时的速度将发生变化，进而影响到炉料在空区的运动轨迹和落点。

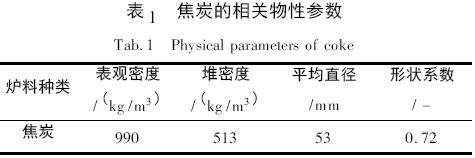
下面以焦炭为例，主要从科氏力的角度出发，解析不同布料操作条件下科氏力对炉料离开溜槽末端的速度以及主落点位置的影响规律。计算所需焦炭的相关物性参数如表1 所示，装料操作参数和部分设备参数如表2 所示。其中煤气流速度为高炉正常操作条件下炉顶煤气的平均流速。

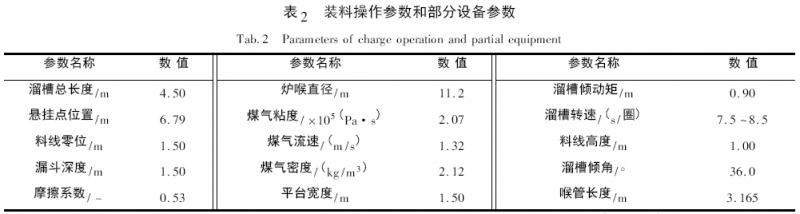
2． 2 科氏力和溜槽长度对焦炭出口速度的影响

料流运动轨迹子模型计算结果表明，受科氏力影响溜槽总长度LT与焦炭出口速度V－coke的关系如表3 所示。

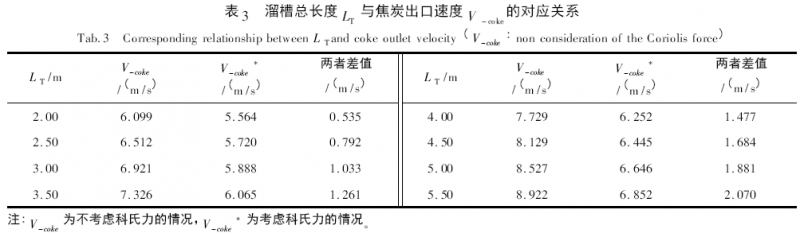
图2 所示为受科氏力作用，溜槽总长度L T与焦炭出口速度V－coke的关系。由图2 可以看出，无论是否考虑科氏力，随溜槽长度的增加，焦炭出口速度均呈现线性增加的趋势。但是受科氏力的影响，在相同溜槽长度时，焦炭的出口速度明显降低，且降低幅度随溜槽长度的增加而增加。京唐公司高炉的溜槽总长度为4． 50 m，在不考虑科氏力时，焦炭的出口速度为8． 129 m /s; 考虑科氏力时，焦炭的出口速度为6． 445 m /s，其差值达1． 684 m /s。

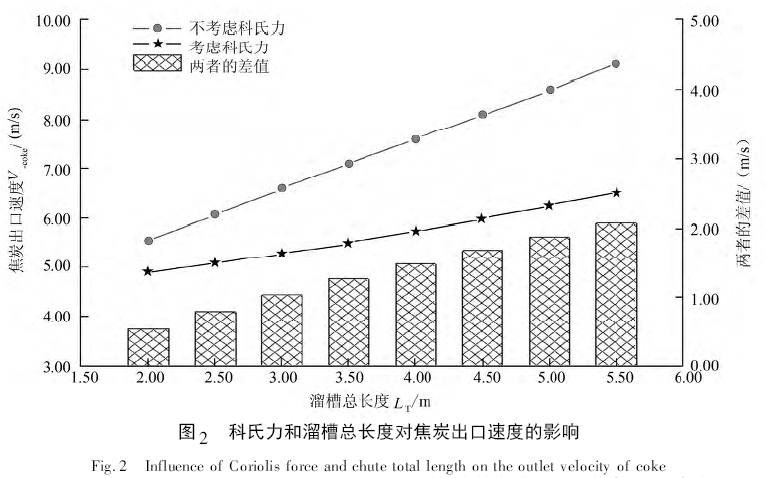
2． 3 科氏力和溜槽倾角对焦炭出口速度的影响

料流运动轨迹子模型计算结果表明，受科氏力影响，溜槽倾角α 与焦炭出口速度V－coke的关系如表4 所示。

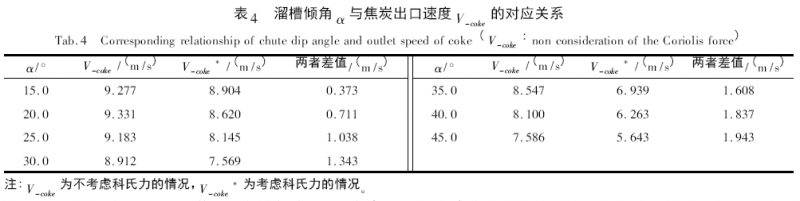
图3 所示为受科氏力作用，溜槽倾角α 与焦炭出口速度V－coke的关系。

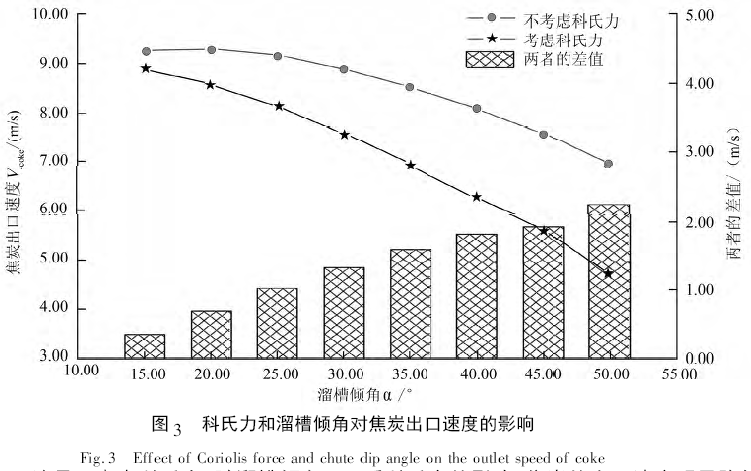
由图3 可知，无论是否考虑科氏力，随溜槽倾角的提高，焦炭出口速度均呈现总体减小趋势。在溜槽倾角较大时，焦炭出口速度对溜槽倾角的变化更加敏感; 相反，则敏感性变差。在相同溜槽倾角时，受科氏力的影响，焦炭的出口速度明显降低，且降低幅度随溜槽倾角的提高而增加。京唐公司大型高炉的溜槽倾角40°时，在不考虑科氏力时，焦炭的出口速度为8． 1 m /s; 考虑科氏力时，焦炭的出口速度为6． 263 m /s，其差值达1． 837 m /s。

2． 4 科氏力和料线高度对焦炭主落点的影响

通过料流运动轨迹子模型计算结果表明，受科氏力影响，料线高度SL 与焦炭主落点位置MSP － coke的关系如表5 所示。

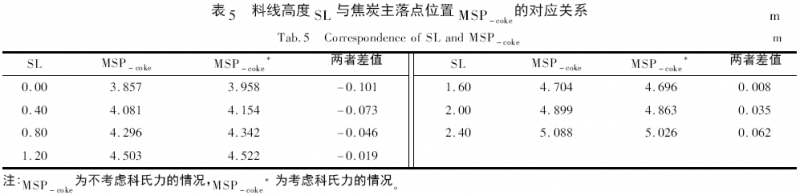
由于焦炭离开溜槽时的速度差异导致炉料在空区运动过程中的料流轨迹的不同，从而进一步表现为焦炭主落点位置MSP － coke的差异。受科氏力作用，料线高度SL 与焦炭主落点位置MSP － coke的关系如图4 所示。

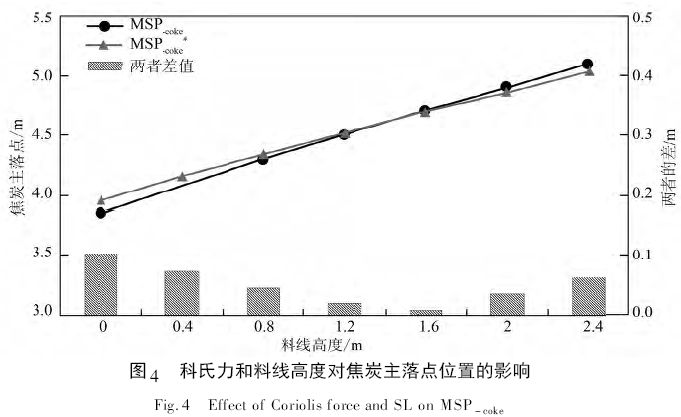
随料线高度的增加，焦炭主落点均呈现不同程度的增加; 但是在低料线时( 小于2 m) ，受科氏力的影响焦炭落点靠近高炉边缘; 在料线较深时( 大于2m) ，受科氏力的影响焦炭落点靠近高炉中心。这主要是因为受科氏力作用，一方面炉料在溜槽出口断面上的形状发生偏转，带来主料流出口位置的提高，从而使炉料靠近高炉边缘; 另一方面，炉料在溜槽出口处的速度降低导致炉料在空区运动过程中的X、Y、Z 方向的初始速度下降，其中X、Y 方向上的速度下降是促进炉料主落点靠近高炉中心的因素，而Z方向速度的下降则是促进炉料主落点靠近高炉边缘的因素。在料线高度SL 较低时，Z 方向的初始速度的影响更大，因此炉料主落点位置更靠近边缘; 反之，在料线高度SL 较深时，X、Y 方向上的初始速度影响更大，因此炉料主落点位置更靠近中心。

2． 5 科氏力和溜槽倾角对焦炭主落点的影响

通过料流运动轨迹子模型计算结果表明，受科氏力影响，溜槽倾角CA 与焦炭主落点位置MSP － coke的关系如表6 所示。

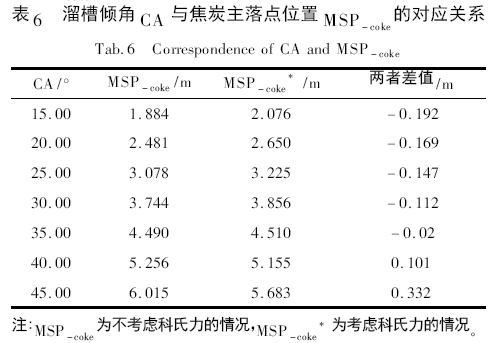
图5 为受科氏力作用，溜槽倾角CA 与焦炭主落点位置MSP － coke的关系。无论是否考虑科氏力，随溜槽倾角的提高，沿炉喉半径方向的焦炭落点均呈增加的趋势。随着溜槽倾角的增加，焦炭主落点位置有不同程度的增加。如: 在不考虑科氏力时，溜槽倾角增加1° 导致焦炭主落点位置大约上升0． 136 m; 在考虑科氏力时，溜槽倾角增加1°导致焦炭主落点位置大约上升0． 120 m。

另外值得注意的是: 在溜槽倾角较小时，受科氏力的影响炉料主落点位置更靠近高炉边缘; 反之，在溜槽倾角较大时，受科氏力的影响炉料主落点位置更靠近高炉中心。这主要是因为在溜槽倾角较小时，炉料的出口速度更大，受科氏力作用的偏转更显著，炉料主料流的出口位置显著提高，从而使炉料主落点位置靠近边缘。随着溜槽倾角变大，炉料在空区的下落距离拉大，其效果相当于料线加深，导致炉料主落点位置在倾角较大时靠近高炉中心。

2． 6 科氏力和溜槽转速对焦炭主落点的影响

通过料流运动轨迹子模型计算结果表明，受科氏力影响，溜槽旋转速度ω 与焦炭主落点位置MSP － coke的关系如表7 所示。

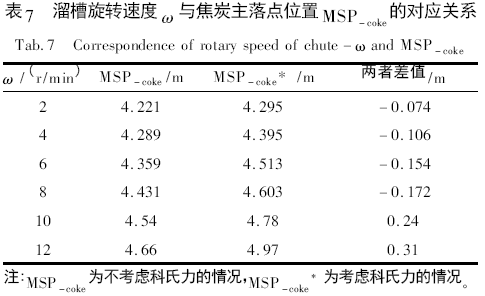
图6 为受科氏力作用，溜槽转速ω 与焦炭主落点位置MSP － coke的关系。无论是否考虑科氏力，随溜槽转速的提高，沿炉喉半径方向的焦炭落点均呈增加的趋势。值得注意的是在溜槽转速较低时，科氏力的作用效果降低; 反之，科氏力的作用效果增加。因此，在溜槽转速较高时科氏力的影响是不容忽略的。

2． 7 科氏力和溜槽总长度对焦炭主落点的影响

炉料在溜槽出口处的出口速度对其在空区的运动轨迹影响较大。由于炉料在溜槽上运动过程中受到科氏力的作用，降低了炉料在溜槽出口处的出口速度，因此对炉料最终的主落点位置也会产生影响。通过料流运动轨迹子模型计算结果表明，受科氏力影响，溜槽总长度L T与焦炭主落点位置MSP － coke的关系如表8 所示。

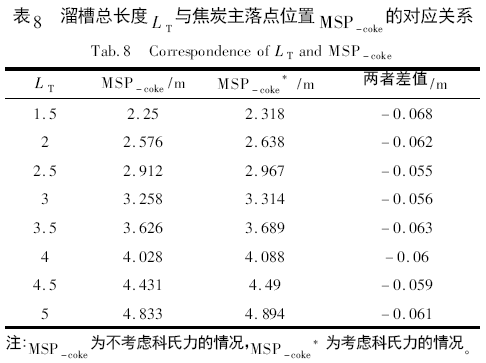
图7 为受科氏力作用溜槽总长度与焦炭主落点的关系。由图7 可知，随着溜槽总长度的增加，焦炭主落点位置也增大，总体而言，溜槽总长度增加0． 5m，焦炭主落点位置增加0． 37 m。在溜槽倾角CA为36°，料线高度SL 为1． 00 m 时，受科氏力的影响焦炭的主落点位置大约提高0． 06 m，并且在不同的溜槽总长度下，科氏力均有一定的作用效果。因此，在不同大小的高炉上开发布料模型的时候都应该充分考虑科氏力的影响。

3 结论

根据炉料在旋转溜槽运动过程的实际情况，建立相应的运动方程和数学模型，充分考虑了科氏力对料流轨迹的影响，丰富了现有布料规律的认识内容并对现场布料起到重要参考作用。

( 1) 受科氏力的作用，炉料在溜槽出口处的速度降低，且溜槽总长度越长、布料倾角越大时的作用效果更加显著。

京唐高炉溜槽长度达到4． 5 m，在不考虑科氏力时，焦炭的出口速度为8． 129 m /s; 考虑科氏力时，焦炭的出口速度为6． 445 m /s，其差值达1． 684m /s，受出口速度降低的影响，在确定料线深度条件下，实际的落点将相对远离炉墙。

京唐高炉的溜槽倾角40°时，在不考虑科氏力时，焦炭的出口速度为8． 1 m /s; 考虑科氏力时，焦炭的出口速度为6． 263 m /s，其差值达1． 837 m /s。

( 2) 科氏力的作用使溜槽内炉料发生偏转升高，对主料流轨迹和落点位置产生影响，在溜槽转速越快时作用的效果越大。

京唐高炉溜槽8． 5 s 旋转1 圈，约7． 06 r /min，不考虑科氏力作用，焦炭落点位置4． 431 m，考虑科氏力作用，焦炭落点位置4． 603 m，相差0． 172 m。

参考文献

［1］陈令坤，于仲洁，周曼丽． 高炉布料数学模型的开发及应用［J］．钢铁，2006，41( 11) : 13．

［2］滕召杰，程树森，赵国磊． 溜槽截面形状及参数对高炉布料的影响［J］． 钢铁，2011，46( 12) : 15．

［3］赵国磊，程树森，徐文轩，等． 高炉中心加焦炉料分布机理及布料方式探讨［J］． 钢铁，2016，51( 6) : 10．

［4］ 任廷志，赵静一，乔长锁，等． 炉料的潜体阻力对高炉布料的影响［J］． 钢铁，1998，33( 5) : 9．

［5］ 滕召杰，程树森，赵国磊． 溜槽截面形状及参数对高炉布料的影响［J］． 钢铁，2014，49( 9) : 34．

［6］ 于要伟，白晨光，梁栋，等． 无钟高炉布料数学模型的研究［J］．钢铁，2008，43( 11) : 26．