孙刘恒^１ ，陈培荣^２

（ 1．中冶华天工程技术有限公司，江苏 南京210019  ；

2．福建三钢闵光股份有限公司，福建 三明365000）

摘要：高炉布料溜槽是无钟高炉炉顶装料设备中的核心部件之一；针对当前生产中常用的半圆形截面溜槽和矩形截面溜槽，分别建立了布料三维数学模型。基于实际高炉参数，计算分析了两种型式溜槽对并罐式无钟高炉布料过程影响，结果表明相比半圆形截面溜槽，矩形截面溜槽布料时料流宽度较小，更加集中，在料面上圆周落点分布及流量分布更为均匀。

关键词：装料设备；无钟高炉；布料；半圆形截面溜槽；矩形截面溜槽

1 概 　 述

旋转布料溜槽是无钟高炉炉顶装料设备中的核心部件之一，对控制和调节炉内炉料分布起着决定性作用，因此国内、外学者对无钟高炉溜槽布料规律进行了大量研究，其中通过布料数学模型研究布料规律是重要研究手段之一^［1-4］。

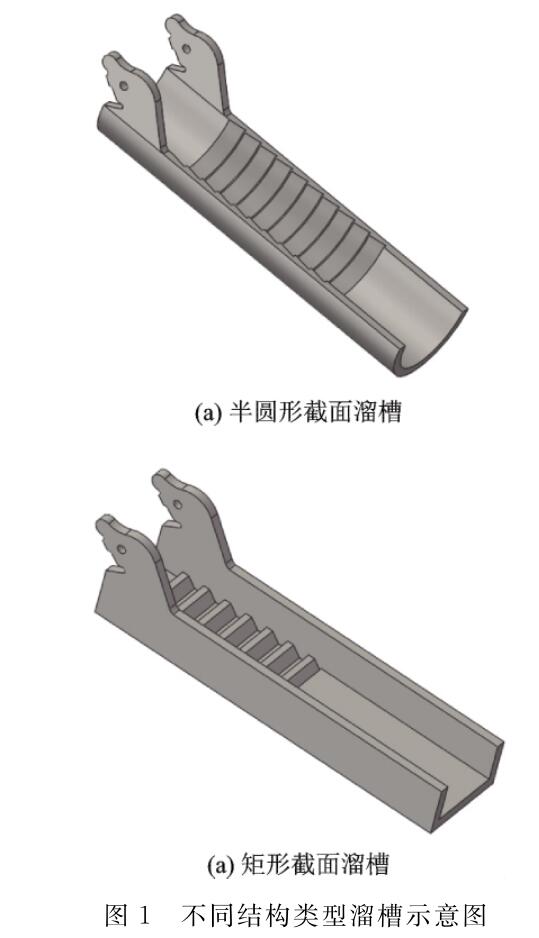
自无钟高炉炉顶应用以来，半圆形截面（或弧形截面）布料溜槽在生产应用中占据着主导地位，随着布料装备的发展，溜槽结构型式也变得多样化，其中矩形截面溜槽在生产中愈加被广泛采用，两种型式溜槽示意图如图1所示。溜槽结构型式的差异必然导致布料规律的不同，目前已有的研究大多局限于半圆形截面溜槽的布料机理，而对矩形截面溜槽布料规律研究较少，尤其对于在复杂的并罐式无钟炉顶布料过程中两者布料规律差异认识存在不足^［5］。

本文通过分析炉料颗粒在布料溜槽内的运动机理，分别建立半圆形截面溜槽和矩形截面溜槽布料的三维数学模型，并应用数学模型对比分析了并罐式无钟布料过程中两种型式溜槽对应的炉料运动及分布行为，为溜槽设计选型和生产操作提供理论指导。

2 建立布料数学模型

2.1半圆形截面溜槽

在高炉多环布料过程中，可通过溜槽自身圆周旋转和倾动两种复合运动将炉料布至炉内指定位置。通过分析炉料在溜槽非惯性系内的运动，其受到的作用力主要包括：1）重力mg；2）支持力F_N；3）摩擦力F_f==_μF_N ；4）牵引惯性力F_e，其中又可分为由动参考系运动产生的惯性力F_e，1=-ma_P，由溜槽非匀速倾动产生的惯性力F_e，2=-ma_t×r₂，由溜槽水平圆周旋转产生的离心力F_e，3=-mω₁×（ω₁×r₁）由溜槽倾动旋转产生的离心力F_e,₄=-mω_２×（ω₂×r₂）；5）科氏惯性力，又可分为由溜槽水平圆周旋转产生的科氏力F_C,₁=-2_m（ω₂×v）和由溜槽倾动旋转产生的科氏力F_C,₁=-2_m（ω₂×v）。

以上式中 μ 为炉料摩擦系数；ω₁ ，ω₂分别为溜槽水平圆周旋转和倾动旋转的角速度（rad/S）；a_t为溜槽倾动角加速度rad/S²）；r₁，r₂分别为炉料颗粒距溜槽水平圆周旋转中心轴和倾动中心轴的矢径（m）；v为炉料颗粒相对运动速度（m/s）。

对于半圆形截面溜槽，炉料颗粒在溜槽内运动过程中不仅沿其轴向向末端运动，同时在溜槽横截面上也发生圆周偏转运动，因此可将炉料复合运动分解为轴向运动和圆周切向运动分别进行分析。图2为炉料颗粒在半圆形截面溜槽内运动过程。

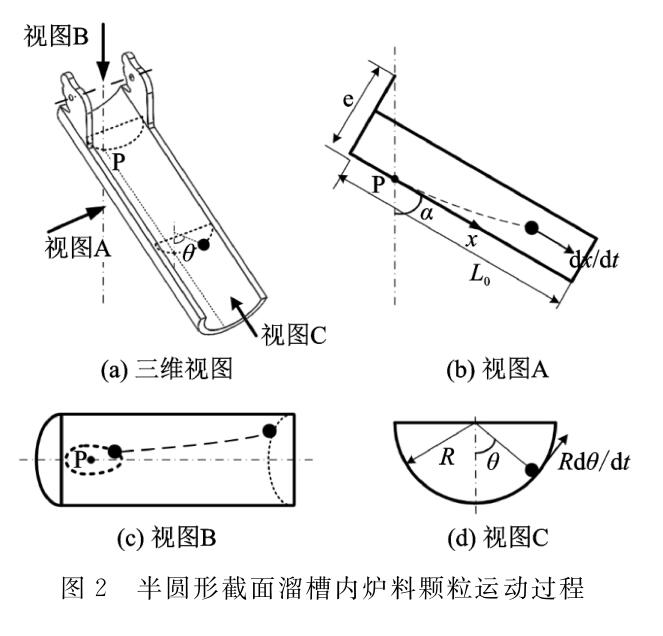
根据运动学原理，建立炉料运动力学方程，并将作用力分别沿溜槽轴向（长度方向）和截面圆周切向进行分解。

在溜槽轴向方向上，炉料颗粒的运动方程为

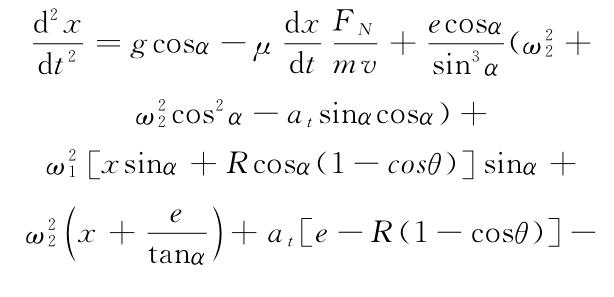
式中a为溜槽倾角（°）；θ为炉料在溜槽横截面上圆周偏转角度（°）；e为溜槽倾动距（m）； Ｒ 为溜槽横截面半径（m）；m为炉料质量（kg）。

2.2矩形截面溜槽

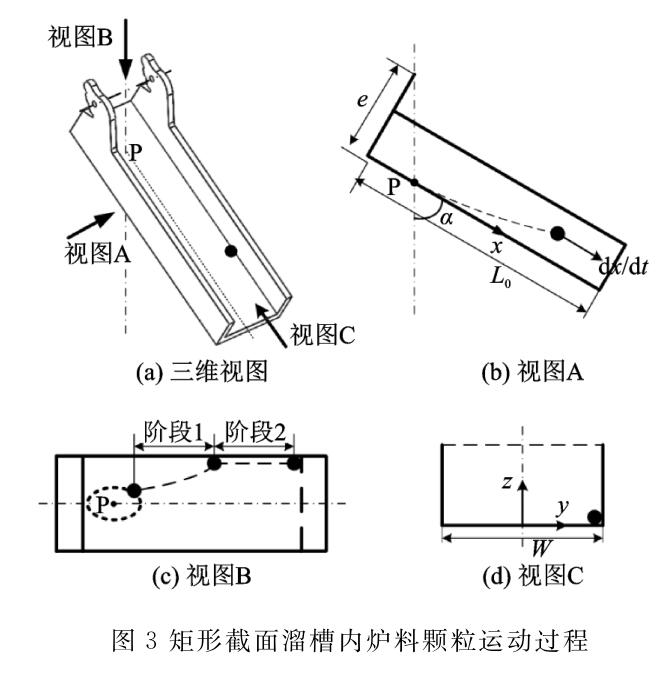
对于矩形截面溜槽，根据炉料运动特点，可将炉料颗粒复合运动分解为沿溜槽长度方向（x方向）和宽度方向（y方向）的运动，运动分解过程如图3所示。

根据炉料运动受力特点，可将运动过程分为两个阶段：“阶段1”为炉料颗粒从在溜槽内落点位置运动至侧壁的过程，此时颗粒同时沿x方向和y方向运动；“阶段2 ”为颗粒碰撞溜槽侧壁后不再发生横向运动，仅沿侧壁向溜槽末端进行x方向运动的过程。其中，“阶段1”为炉料运动必经阶段，而“阶段2”过程在溜槽转速较小时可能不存在，即炉料始终未碰撞侧壁即已流出溜槽。

基于炉料颗粒运动过程受力综合分析，“阶段1”过程中炉料颗粒沿x方向和y方向的运动方程分别为：

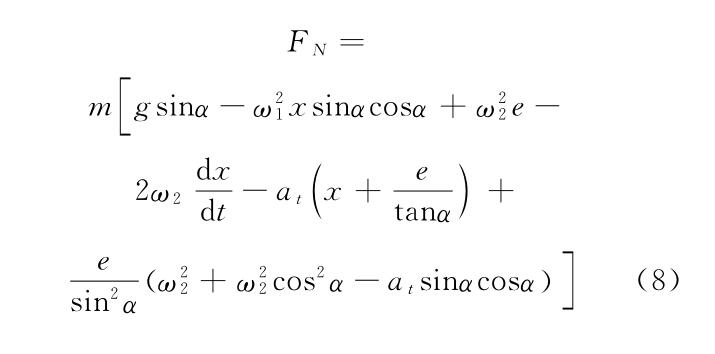
3布料规律对比分析

为了对比分析半圆形截面溜槽与矩形截面溜槽布料的差异性，基于某并罐式无钟高炉炉顶实际的设备参数和操作参数，计算了布料过程中炉料运动及分布状况。

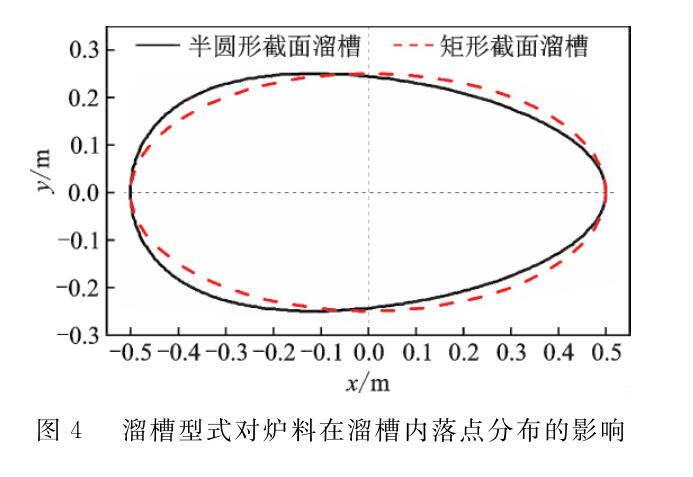
由于溜槽内型截面形状的差异，炉料从中心喉管落至溜槽内的落点分布也会有所差异，造成溜槽内炉料初始运动状态的差异。图4为 a=30°布料时炉料在半圆形截面溜槽和矩形截面溜槽内的落点轨迹分布二维投影形状。图中x方向为溜槽长度方向，y方向为溜槽宽度方向，可见半圆形截面溜槽内炉料落点轨迹投影形状为非标准椭圆形，而矩形截面溜槽内的落点形状为椭圆形，且两者在x方向和y方向最大落点距离均相同，分别为 0.5m和0.25m 。由此可见，溜槽型式差异造成了炉料在溜槽内初始落点分布的差异，并将导致炉料在溜槽内运动历程的不同，从而对整个料流轨迹和炉内料面上炉料落点分布产生影响。

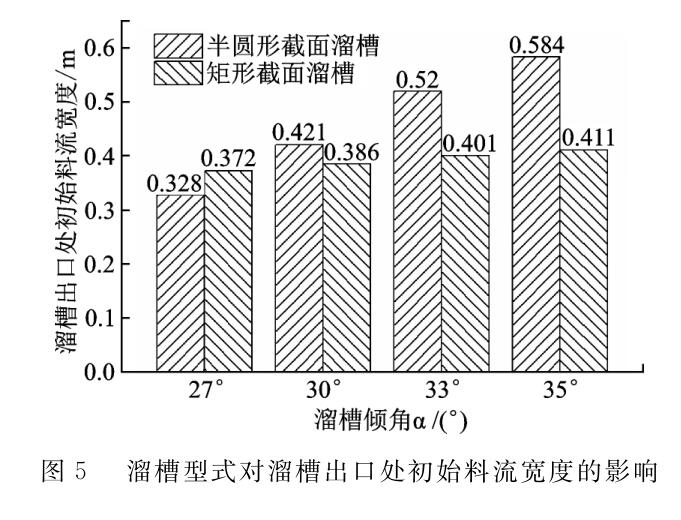
溜槽型式除了影响炉料在溜槽内初始落点分布及运动历程，对溜槽出口处的初始料流宽度也有影响，图5给出了半圆形截面溜槽和矩形截面溜槽布料角度依次取27°，30°，33°和35°时溜槽出口处的初始料流宽度数值。从图中可见，除在较小角度a=27°布料时矩形截面溜槽出口处料流宽度稍大于半圆形截面溜槽出口处料流宽度，在a=30°，33°和35°等较大角度布料时矩形截面溜槽对应料流宽度均小于半圆形截面溜槽，且随布料角度增大，前者增幅较小，后者增幅较大，两者差值不断增大。由此可知，矩形截面溜槽布料有利于减小料流宽度，使得料流更加集中，半圆形截面溜槽采用不同档位布料时料流宽度波动较大。

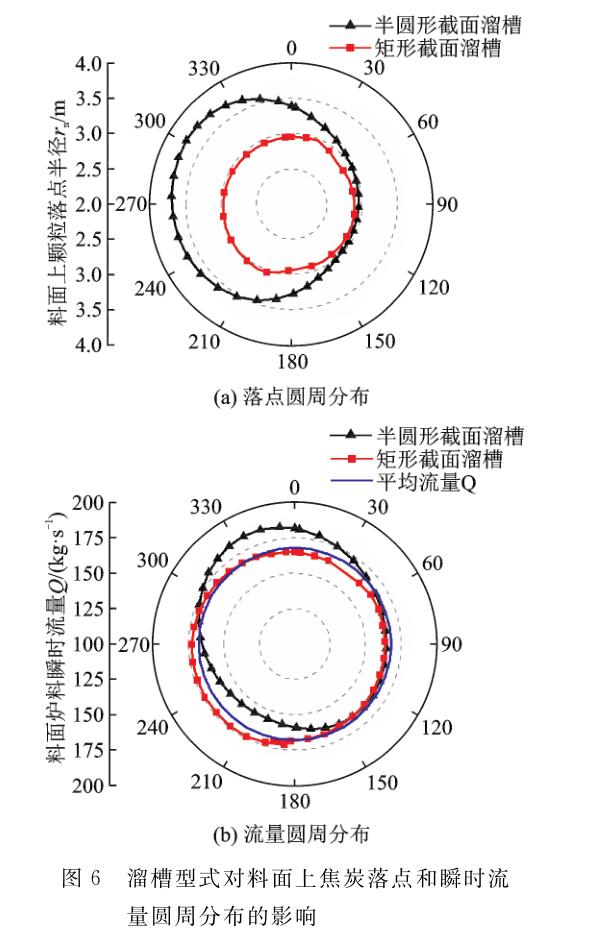
在整个布料过程中，前序环节的差异必将导致最终炉内炉料分布的差异。图6 进一步给出了半圆形截面溜槽和矩形截面溜槽布料时焦炭在炉内料面上的落点以及瞬时流量圆周分布状况。从图6（a）可知，采用矩形截面溜槽布料时焦炭平均落点半径约为3.01m，半圆形截面溜槽对应的平均落点半径约为3.36m ；两者均显示出明显的圆周分布不均匀性，但半圆形截面溜槽布料时落点半径最大值与最小值差值高达0.79m ，而矩形截面溜槽仅为0.20ｍ ，表明矩形截面溜槽布料过程中炉内炉料落点圆周偏心远小于半圆形截面溜槽。

从图6（b）中料面上焦炭瞬时流量圆周分布可看出，矩形截面溜槽布料时瞬时流量圆周分布曲线与平均流量曲线较为接近，而半圆形截面溜槽对应的瞬时流量分布曲线偏差较大，表明矩形截面溜槽布料也有利于减小炉料流量的圆周偏心。

4结束语

1）针对当前生产中常用的半圆形截面溜槽和矩形截面溜槽，基于布料过程受力分析，分别建立了两种型式溜槽布料三维综合数学模型，深入解析了溜槽布料过程中炉料运动分布机理。

2）利用建立的数学模型计算分析了两种型式溜槽布料差异性，结果表明：炉料在半圆形截面溜槽内落点轨迹投影形状为非标准椭圆形，而在矩形截面溜槽内的落点形状为椭圆形；矩形截面溜槽布料有利于减小料流宽度，使得料流更加集中，而半圆形截面溜槽布料时在不同档位料流宽度差异较大；半圆形截面溜槽布料时炉料圆周平均落点半径略大于矩形截面溜槽，且落点半径圆周偏差远高于后者，此外其炉料流量圆周分布不均匀程度也显著高于后者，表明矩形截面溜槽布料更有利于减小炉料圆周分布偏心。