舒佳

(河钢集团唐山钢铁股份有限责任公司冷轧薄板厂唐山 063000)

【摘要】冷轧镀锌线带钢张力控制是生产中十分重要的环节，通过对基于钢种分组以及带钢规格数据匹配，用获得的匹配值对计算值进行修正，并用线性差值算法求解对应的参数设定值以稳定控制张力。

【关键词】过程控制；算法；模型

1唐钢冷轧镀锌二级系统概述

在冷轧带钢生产的镀锌处理线，过程控制系统是衔接制造执行系统(MES)和现场控制器(PLC)的重要一环，对生产节奏的把控、各机械设备、生产环节参数的设定以及生产数据的统计起着至关重要的作用。过程控制系统的核心功能模块是设定参数计算的数学模型。由于原生产线在设计之初考虑的产品种类单一、现场情况简单,其数学模型不能支撑当前需求，造成参数设定普遍采用粗放式的设定方法，不能充分结合产品特性以及历史生产数据而定，导致生产精度偏低，需要较多的人工干预。

针对当前小批量、多品种的订单需求，设计一种充分考虑钢种类型的生产工艺数学模型，并结合相关机理模型组成一种新型的镀锌线过程控制方法,该控制方法通过模型和算法，为位于不同生产环节的机械设备计算设定值成为亟待解决的课题。

2技术方案

2.1钢种分类算法

构建隶属度函数，决定钢种归属类别。入口钢种属性记为X₁ ,出口钢种属性记为X₂，则该钢种属性组合X =X₁+X₂,其隶属度函数记f(X)=f(X₁) +f(X₂),根据隶属度函数值,将该钢种组合进行归类：

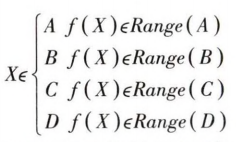
上述算法描述了该控制方法对钢种进行分类的过程，为后续的分组计算设定值做好铺垫。钢种分类算法过程如图1所示：

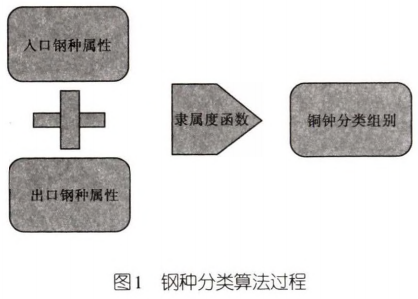
2.2根据钢种组别以及PDI数据建立工艺参数线性模型

当确定钢种组别之后，需要进行各环节设备设定值的计算。通过静态表形式描述各工艺参数在常用规格节点上的设定值，基于静态表建立分段线性函数，描述该工艺参数在规格范围内的分布（见图2）。以入口活套张力这一参数为例说明该过程：

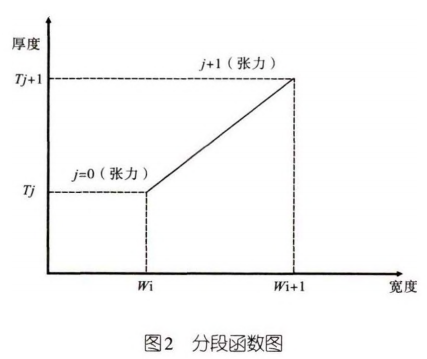
带钢宽度向量记为W=（W₁,W₂,…W_m）,其中m表示带钢宽度节点数；厚度向量记为T = （T₁,T₂,…T_n）,其中n表示带钢厚度节点数。则在节点（W_i，T_j）处，带钢的活套入口张力为T_enij,在节点（W_i,T_j）与（W_i+1，T_j+1)之间的张力函数表达式如下：

线性差值算法表达式如下

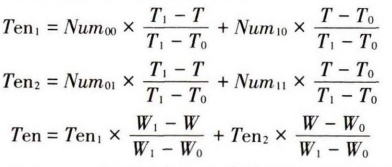
其中：Ten表示厚度为T，宽度为W的带钢在入口活套处的张力值。N_um00, N_um10, N_um01 , N_um11分别表示不同规格组合的张力值。T₁，T₀，W₁，W₀分别表示图2中横纵坐标中的四个张力和厚度数值。

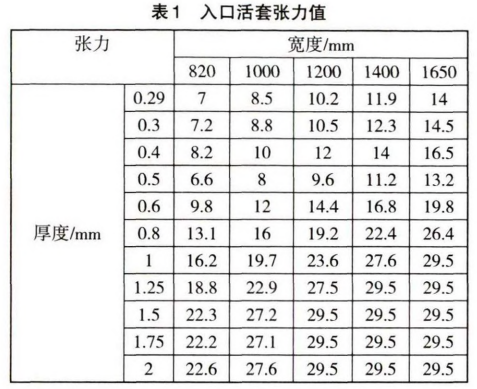
带钢不同的张力和厚度组合所对应的活套入口张力数值由表格形式给出，如表1所示：

2.3支撑工艺参数线性模型的机理模型

工艺参数的计算模型需要轧制机理模型的支撑.如表1中每种规格组合的入口活套张力值均由张力计算机理模型得出。张力机理模型如下^[1]：

张力的产生：带钢上之所以有张力的作用是因为在带钢长度方向上存在速度差，使带钢在不同部位处的金属有相对位移而产生张力，平均单位张力σ_Tm,带钢的横截面积为A，作用在带钢上的张力值Ten计算公式如下：

Ten =σ_Tm A

平均张力σ_Tm与弹性应变ɛ成正比关系：

σ_Tm = Eɛ

其中E为材料的弹性模数，对于带钢E =20.58 x 10⁴ MPa。

弹性应变ɛ由如下公式表示：

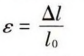
其中∆l表示带钢在长度方向上的位移量，l₀表示带钢上任意两点之间的距离，也称为标准距离。

3线性网络模型优化模型

建立工艺参数线性模型，可以通过线性差值算法求岀相同钢种情况下，不同规格组合带钢的参数设定值，通过大规模生产，可以得出针对某一项参数的完整的线性分段函数。同样以活套入口张力值为例，经过大规模生产之后，可得到如图3所示的分段函数：

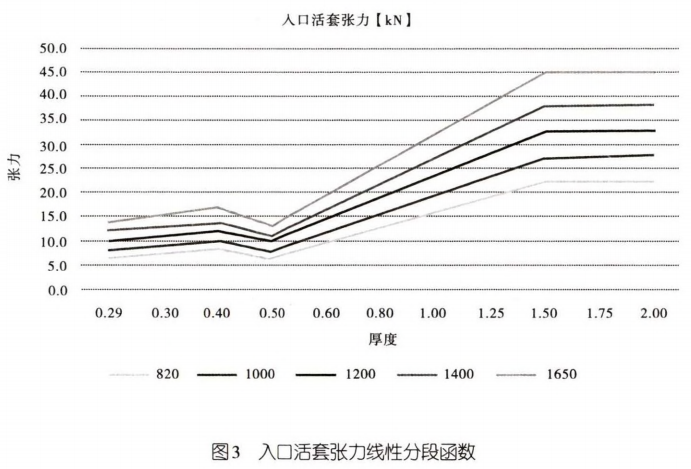
对于上述线性分段函数，可以获得若干离散的数据，根据这些数据，有必要得到一个连续的函数（也就是曲线）与已知数据相吻合.也就是对现有的分段线性函数进行拟合。该控制方法中采用最小二乘法多项式曲线拟合算法进行拟合，从而得到平滑的曲线。该过程通过以离线的形式定期进行。

多项式形式如下：

φ（x） = ax⁵ + bx⁴ + ex³ + dx² + ex +f

其中φ（x）代表入口活套张力值Tension的连续函数，x代表带钢厚度Thickness（此公式需要固定带钢厚度）。

最小二乘法原理如下^[2]： 

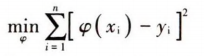
其中（x_i，y_i）表示各离散的带钢规格组合，n表示规格组合个数。

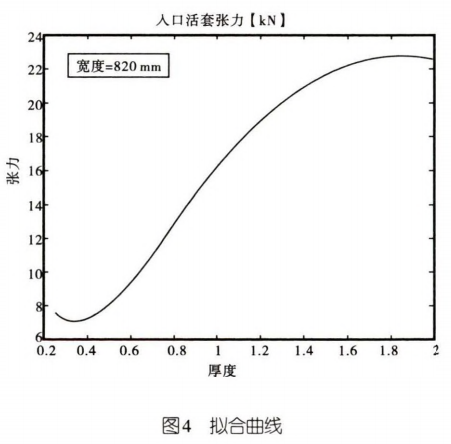
最终拟合得到的曲线如图4所示（选取带钢宽度 Width=820 mm 为例）。

4结语

此种带钢镀锌线过程控制方法的投入使用，大大提升了镀锌线的过程控制水平，更高地满足了生产精度，同时完善了镀锌产线的过程控制系统，提高了生产线工人的使用便捷性，大大降低了误操作与次品率，更加精准的生产数据与产品信息也为信息化系统提供了强有力的支撑。

参考文献

[1]丁修埜.轧制过程自动化[M].北京：冶金工业出版社, 2013:314-317.

[2] 田珑，刘宗田.最小二乘法分段直线拟合[J].计算机科学.2012.S1.