于要伟 白晨光 梁 栋
（重庆大学冶金系 ）
摘 要 建立高炉无料钟布料模型的技术路线可以分成三类 ：物理模型试验研究、经典力学理论和人工智能技术。本文结合国内外无料钟炉顶布料模型‚对这三类技术路线的运用过程进行详细的阐述‚总结出这三类技术路线的优缺点‚并针对其缺点提出了相应的改进措施。
关键词 无料钟布料；物理模型试验研究；经典力学理论；人工智能技术
1 前言
随着高炉容积大型化和炉顶压力的不断提高‚钟式炉顶布料已不能满足灵活布料和密封的需要。而无料钟炉顶溜槽布料灵活‚可以实现单环布料、多环布料、螺旋布料和定点布料；设备密封性好‚现逐步取代钟式炉顶。布料制度决定着炉料在炉内的初始分布‚炉料的初始分布对炉料下降、煤气流分布、煤气利用、高炉顺行和长寿有重要作用。而在传统高炉操作中‚操作人员通过探尺、煤气成分检测和操作经验等估计炉料在炉内的分布情况‚因此对正确反映炉料的分布情况具有很强的主观性和经验性。
另外虽然炉顶温度、十字测温、炉顶摄像等装备已经在许多高炉上得到了推广与应用‚但是基于这些监控设备 （尤其是炉顶摄像装置 ）的检测手段尚不完善‚对于生产指导多为定性方面的‚无法对上部装料制度做出准确的判断。由此可见‚建立无料钟布料数模的意义十分重大。 从 20世纪 60年代以后‚国内外许多冶金人士研究了无料钟高炉布料‚提出了许多的布料模型。 这些模型虽然采用了不同的技术路线‚但是所采用的技术路线大体上可以分成三类：物理模型试验研究、经典力学理论、人工智能技术。本文从这三类的总体路线、优缺点、所用的数学方法等几个方面‚对国内外无料钟溜槽布料模型进行阐述。
2 物理模型试验研究
物理模型试验研究的总体路线是：用某座具体高炉上部 （炉身、炉喉、炉顶设备等 ）缩小模型‚模拟高炉无料钟布料全过程。试验中考察溜槽倾角 α、溜槽转速 ω、节流阀开度 γ、料线 ｈ、批重 ｐ等装料制度的主要操作参数分别对炉料堆尖的位置 Ｎ（Ｎｘ‚ Ｎｙ）、料面堆角 （料面中心角 θ1 和料面边缘角 θ2）、 粒度径向分布和气流分布等料面形状参数的影响。
从试验中得到装料制度操作参数和料面形状参数的大量数据‚然后通过数学方法找到这两组数据之间的关系‚最后把这种数学关系通过修正 （或不用修正 ）‚用于相应的高炉生产上。见表 1。
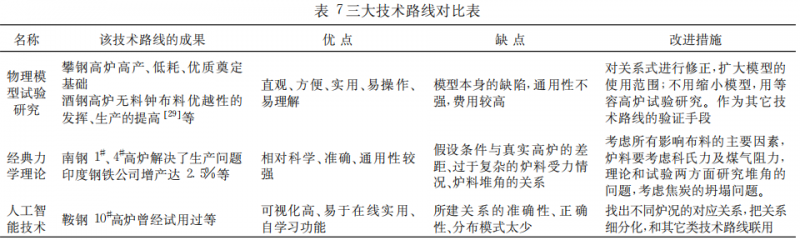
从表 1总结出来的优缺点‚可以看出‚该技术路线的主要问题是模型通用性不强和试验费用较高。因为物理模型是以某座高炉的具体条件为基础‚按照相似原理组建起来的‚试验结果有很强的针对性；试验设备的购买及试验次数很多‚自然会增加试验费用。表 1里有关物理模型试验研究的优缺点是针对该技术路线所建立的模型而言‚和其它技术路线相比较的结果。比如方便‚若是给定 ｈ值‚就可以直接从所建关系式找到相应的炉料粒度分布、或炉料位置。模型直观是指物理试验研究本身比其它技术路线更直接‚可以真实地看到布料全过程。
3 经典力学理论
经典力学理论的主要路线是：把炉料在布料过程的运动当成质点的运动。该运动过程可以分解成三大步骤：炉料从节流阀流出到溜槽前的运动、炉料在溜槽上的运动、炉料从溜槽末端流出到炉喉料面前的运动及炉料落点的形成。通过各种方法解出各个步骤炉料的初速度‚再根据力学理论‚列出本步骤的运动方程‚从中解出炉料的末速度。该速度作为下个步骤的初速度。这样反复求解‚最终可以求出炉料的落点及新的料面形状。
3．1 炉料从节流阀到溜槽前的运动
开炉前测得炉料流量 Ｇ和γ的多组数据‚用数学方法把这些数据回归出两者之间的关系 （见表 2）‚再根据水力学中的连续性方程‚就可以求得炉料出节流阀时的速度Ｖ0与 γ的关系：
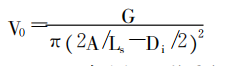
式中 Ａ———节流阀投影面积；
Ｌｓ———节流阀周边边长。
Ａ、Ｌｓ与 γ的关系见文献 ［7］。表 2里 Ｇ和 γ或 Ｇ和 deff的关系式‚只是研究者基于不同的炉顶设备 （如节流阀规格、炉罐结构 ）和原燃料条件回归出来的数学关系式。同时可以看出这些关系式通用性不是很强‚只能针对相同或相似条件的高炉才能使用。
炉料以初速度 Ｖ0从节流阀流出‚经过下密封阀、波纹管、眼镜阀和中心喉管等最后落到溜槽上。在这个过程里‚由炉料运动方程可得炉料入溜槽前的速度Ｖ1或是直接由库仓公式推导出来 Ｖ1（见表 3）。
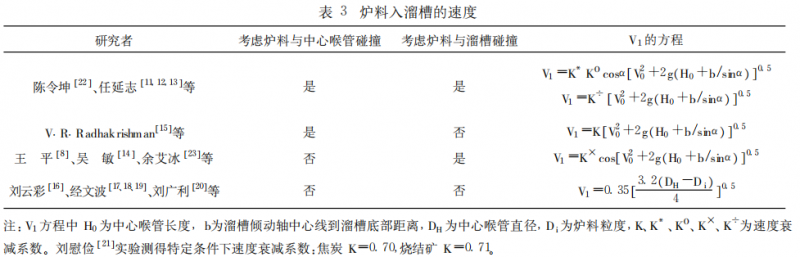
从表 3可以看出‚陈令坤和任延志都考虑了炉料与中心喉管及炉料与溜槽的碰撞‚只是方程的形式不一样而已‚Ｋ÷相当于 K ∗ ＫＯcosα。而任延志和Ｖ．R．Radhakrishman的方程形式虽然一样‚但是物理意义却相差很大。还可以看出由运动方程解出的要比直接由库仓公式导出的 Ｖ1更精确、合理。
3．2 炉料在溜槽上的运动
炉料在溜槽上的运动受到诸多力的作用‚做变加速滑落运动。这些力分别是：①重力 （ｍｇ）、②惯 性离心力 （Ｆ1 ＝ω 2ｍ lsinα）、③科氏惯性力 （coriolis force） （Ｆ2 ＝2ｍＶωsinα）、④溜槽对炉料的摩擦力 （μR）、⑤炉料的潜体阻力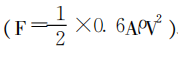
⑥溜 槽对炉料的反作用力 （R＝mgsinα－ω 2lmsinaαcosα）。 其中 ｍ是炉料的质量‚ｌ为炉料在溜槽上的有效长度‚Ｖ是炉料速度。各力的分布见 1图‚其中科氏惯性力与重力‚惯性离心力垂直‚即垂直纸面向外 （图 1中没有标出 ）。
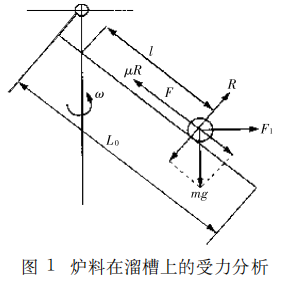
图 1 炉料在溜槽上的受力分析 在求得 Ｖ1 后‚对炉料在溜槽上的运动‚列运动 方程并结合初始条件 （ｌ＝0时‚Ｖ＝Ｖ1‚ｌ＝Ｌ0 －ｂ／ tanα时‚Ｖ＝Ｖ2）可得炉料出溜槽时的速度 Ｖ2。在此 过程中‚因为考虑炉料受力多少的不同 （见表 4）‚虽 然得到 Ｖ2的值相差不大‚但最后对炉料落点的影响会很大。
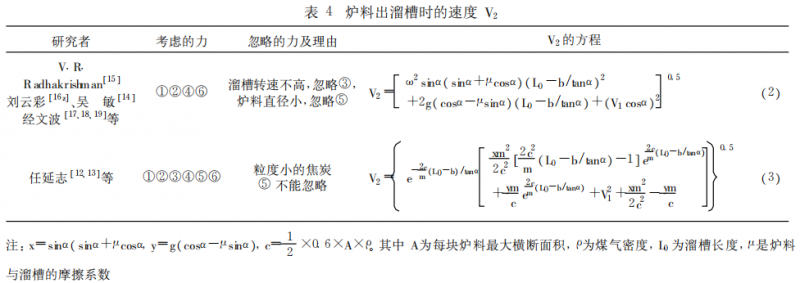
比较表 4炉料出溜槽时的速度‚可知 （3）式考 虑煤气阻力的作用‚计算更接近真实情况‚同时也更 复杂‚且 ｍ是个不易知道的量。Ｍ值的大小肯定对Ｖ2会有影响。
3．3 炉料在炉喉空区的运动
炉料在炉喉空区内运动‚受到重力和煤气阻力（常把此力忽略 ）的双重作用‚当它出溜槽末端的速度 Ｖ2已知后‚它的轨迹可以直接从运动方程解出‚再由运动轨迹就可以求得落点坐标。炉料在溜槽末端的速度分解成三个分量：沿高炉中心线方向 ｚ轴的速度 Ｖｚ＝－Ｖ2cosα‚沿溜槽末端切线方向的速度 Ｖθ＝ω（Ｌ0－ｂ／tanα）sinα‚沿炉喉半径方向的速度 Ｖr ＝Ｖ2sinα。没有考虑煤气阻力的情况下‚分别在三个方向上列出各自的运动方程。三个方向上的运动方程如下：
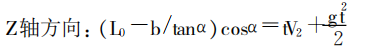
切线方向：θ＝Ｖθｔ
半径方向：ｒ＝（Ｌ0－ｂ／tanα）sinα＋ｔＶ2sinα
建立布料数模的目的是求出炉料在炉内料面的分布情况‚即炉面形状。当炉料的落点和上一批炉料的料面形状已知时‚这时只要求解出炉料的堆角（料面中心角 θ1 和料面边缘角 θ2）‚再结合适当的料面形状假设条件‚就可以求得料面形状。然而在求炉料的堆角时有很大的分歧‚见表 5。
从表 5可以看出不同的研究者求解 θ1 和 θ2 的值相差很大‚由此引起所建模型求得的料面形状也会相差较大。
综合经典力学理论建模的技术路线的全过程‚可以看出以下几点：
（1） 炉料出节流阀的速度 Ｖ0 与节流阀开｀度 γ 关系式模型的建立。在建模时‚不仅要考虑模型的 通用性‚而且还要考虑节流阀常期工作中的磨损情况。基于这两点‚可以考虑用经验公式和人工智能技术相结合的方法。先用经验公式计算‚然后用人 工智能技术作为修正和验证手段。
（2） 炉料入溜槽时的速度 Ｖ1 的求解。不仅要考虑炉料与中心喉管的碰撞‚而且还要考虑炉料与溜槽的碰撞。
（3） 炉料在溜槽上的受力‚不仅要考虑炉料受到重力、离心力、摩擦力、溜槽对炉料的反作用力‚而且还要考虑炉煤阻力和哥氏力对炉料的影响。
（4） 在求解料面形状的时候‚对炉料堆角值的计算‚这是影响料面形状的主要因素。
4 人工智能技术
人工智能技术用于布料的总体路线：煤气流分布、或煤气利用率等反映炉料在炉内分布的物理量分成若干个等级‚并组成标准模式库‚每一个等级对应着一种装料制度。这种对应关系的建立是通过人工神经网格、模式识别等方法来确定的。一旦给定一种物理量模式‚就可以通过人工智能的方法‚找到待识别的模式和标准库里一样的那种模式‚或是较接近 （最优 ）的模式‚从而找到相应的装料制度。反之也然。几种典型模型的对比见表 6。
该技术路线的主要缺点是标准模式库不够完整‚不能全部代表所要表示的关系式。一旦给定一个标准式库里没有训练过的关系式‚不能正确找到所需要的物理量。
5 结论
综上所述‚物理模型试验研究和人工智能技术这两类技术路线‚分别是基于物理试验和人工智能技术找到装料制度参数和炉料在炉内的分布参数之间的直接关系式。它们的共同点是这两组参数之间的关系是一一对应关系。人工智能技术路线优于物理模型试验研究的一点是能吸收新的关系式‚并把这种关系式作为标准库的一部分‚为以后出现相同或类似的模式积累经验‚即自学习功能。 经典力学理论的技术路线不同于其它技术路线的是对这种对应关系的求解方法。此方法不是简单地通过回归 寻优等方法得到两者之间的直接关系式‚而是通过研究布料规律、炉料运动的轨迹及其原理‚加上一定的假设条件‚运用数学和物理学的知识‚求解出来的。该技术路线的最大缺点是在求解料面形状的过程中‚每个步骤都要正确、合理‚否则将会影响到最终结果。
表 7是三类技术路线的对比表。从中不难看出‚这三类技术路线不但各有自已的优缺点‚而且不同技术路线之间的优点是互补的。若两类、或三类技术路线共同或交叉使用‚就可以相互取长补短
参 考 文 献
［1］ 谢国海‚杜鹤桂‚赵正清．攀钢 4号高炉无料钟炉顶烧结矿粒度分布规律及数学模型 ［Ｊ］．钢铁钒钛‚1989‚（2）：20－25．
［2］ 杜鹤桂‚谢国海．无料钟炉顶高炉布料气流分布模拟研究 ［Ｊ］．炼铁‚1989‚（5）：48－53．
［3］ 傅世敏‚王立冬．无钟炉顶布料料面测定及料面数模 ［Ｊ］．炼铁‚1991‚（2）：15－19．
［4］ 傅世敏‚周国凡．湘钢 2号高炉 ＰＷ炉顶料面数学模型应用研究 ［Ｊ］．武汉钢铁学院学报‚1994‚（1）：1－5．
［5］ ＹｏｓｈｉｏＯｋｕｎｏ．ＤｅｖｅｌｏｐｍｅｎｔｏｆａＭａｔｈｅｍａｔｉｃａｌＭｏｄｅｌｆｏｒＢｕｒｄｅｎＤｉｓｔｒｉｂｕｔｉｏｎｉｎａＢｌａｓｔＦｕｒｎａｃｅ．ｉｎ：44ｔｈＩｒｏｎＭａｋｉｎｇＣｏｎｆｅｒｅｎｃｅ‚Ｄｅｔｒｏｉｔ‚ｐｒｏｃ． 1985‚ｐｐ．543－552．
［6］ ＪｕａｎＪＩＭＥＮＥＺ‚ＪａｖｉｅｒＭＯＣＨＯＮ‚ＡｎｔｏｎｉｏＦＯＲＭＯＳＯ‚ｅｔａｌ．ＢｕｒｄｅｎＤｉｓｔｒｉｂｕｔｉｏｎＡｎａｌｙｓｉｓｂｙＤｉｇｉｔａｌＩｍａｇｅＰｒｏｃｅｓｓｉｎｇｉｎａＳｃａｌｅＭｏｄｅｌｏｆａＢｌａｓｔ ＦｕｒａｎｃｅＳｈａｆｔ［Ｊ］．ＩＳＩＪ‚2000‚（2）：114－120．
［7］ 马钢 2500ｍ3高炉无料钟炉顶节流阀特性的研究 ［Ｊ］．炼铁‚1995（3）：37－40．
［8］ 高征铠‚戴建华‚蒋星华等．济钢 1750ｍ3高炉无料钟布料仿真模型 ［Ｊ］．炼铁‚2005‚（5）：33－35．
［9］ 王平．串罐无料钟料流轨迹与宽度测定及其分析 ［Ｊ］．钢铁‚2003‚（3）：8－12．
［10］ Ｋ．Ｙｏｓｈｉｍａｓａ‚Ｔ．Ｊｉｍｂｏ‚Ｔ．Ｊｏｋｏ‚ｅｔａｌ．Ｉｎｖｅｓｔｉｇａｔｉｏｎｓｏｆｂｅｌｌ－ｌｅｓｓｃｈａｒｇｉｎｇｂａｓｅｄｏｎｆｕｌｌｓｃａｌｅｍｏｄｅｌｅｘｐｅｒｉｍｅｎｔｓ‚Ｔｒａｎｓ．ＩＳＩＪ‚24（1984）799．
［11］ 任延志‚盛义平．高炉溜槽布料器的布料规律 ［Ｊ］．钢铁‚1995‚（5）：5－8．
［12］ 任延志‚赵静一‚乔长锁‚等．炉料的潜体阻力对高炉布料的影响．钢铁‚1998‚（5）：1－8．
［13］ 任延志‚金听‚景奉儒．无钟溜槽结构参数对高炉布料的影响．钢铁‚2003‚（11）：9－11．
［14］ 吴敏‚田超‚曹卫华．无料钟高炉布料模型的研究与应用 ［Ｊ］．控制工程‚2006‚（9）：490－493．
［15］ Ｖ．Ｒ．Ｒａｄｈａｋｒｉｓｈｍａｎ‚Ｋ．ＭａｒｕｔｈｙＲａｍ．Ｍａｔｈｅｍａｔｉｃａｌｍｏｄｅｌｆｏｒｐｒｅｄｉｃｔｉｖｅｃｏｎｔｒｏｌｏｆｔｈｅｂｅｌｌ－ｌｅｓｓｔｏｐｃｈａｒｇｉｎｇｓｙｓｔｅｍｏｆａｂｌａｓｔｆｕｒｎａｃｅ［Ｊ］． Ｊｏｕｒａｎｌｏｆｐｒｏｃｅｓｓｃｏｎｔｒｏｌ‚2001（11）：565－586．
［16］ 刘云彩．高炉布料规律 ［Ｍ］．北京：冶金工业出版社‚2005‚24－25．
［17］ 经文波‚陈小雷．无料钟高炉应用数学模型研究 ［Ｊ］．中国冶金‚2004‚（2）：29－32．
［18］ 经文波‚谈云兰．无料钟布料数学模型在南钢高炉布料中的应用 ［Ｊ］．江西冶金‚2006‚（5）：9－12．
［19］ 经文波‚陈小雷．无料钟高炉布料数学模型研究 ［Ｊ］．冶金自动化‚2003‚（1）：29－31．
［20］ 刘广利‚田仙仙．带螺线的无料钟高炉多环布料仿真系统 ［Ｊ］．ｈｔｔｐ：／／ｗｗｗ．ｐａｐｅｒ．ｅｄｕ．ｃｎ‚中国科技论文在线．
［21］ 刘慰俭‚叶肇宽．无料钟高炉炉顶设备中布料的研究工作 ［Ｊ］．钢铁‚1983‚（5）：1－7．
［22］ 陈令坤‚于仲洁‚周曼丽．高炉布料数学模型的开发及应用 ［Ｊ］．钢铁‚2006‚（11）：13－16．
［23］ 余艾冰‚杜鹤桂．高炉无钟炉顶炉料运动的理论解析 ［Ｊ］．东北大学学报‚1986‚（4）：71－78．
［24］ 杨雪峰‚李软．昆钢 6号高炉布料规律研究 ［Ｊ］．炼铁‚2002（ｓ）：26－29．
［25］ 李旭红．无钟炉顶布料规律及其预测模型开发进展 ［Ｊ］．包钢科技‚2000‚（4）：12－14．
［26］ ＭｉｃｈｉｎｏｒｉＨＡＴＴＯＲＩ‚ＢｕｎｇｏＩＩＮＯ‚ＡｋｉｏＳＨＩＭＯＭＵＲＡ‚ｅｔａｌ．ＤｅｖｅｌｏｐｍｅｎｔｏｆＢｕｒｄｅｎＤｉｓｔｒｉｂｕｔｉｏｎＳｉｍｕｌａｔｉｏｎＭｏｄｅｌｆｏｒＢｅｌｌ－ｌｅｓｓＴｏｐｉｎａＬａｒｇｅ ＢｌａｓｔＦｕｒｎａｃｅａｎｄＩｔｓＡｐｐｌｉｃａｔｉｏｎ［Ｊ］．ＩＳＩＪ‚1993‚（10）：1070－1077．
［27］ 姜慧研‚许桂清‚周建常．神经网络专家系统在高炉布料控制中的应用 ［Ｊ］．基础自动化‚2000‚（1）：1－3．
［28］ ＰｅｔｔｅｒｓｓｏｎＦｒａｎｋ‚ＨｉｎｎｅｌａＪａｎ‚ＳａｘｅｎＨｅｎｒｉｋ．Ｅｖｏｌｕｔｉｏｎａｒｙｎｅｕｒａｌｎｅｔｗｏｒｋｍｏｄｅｌｉｎｇｏｆｂｌａｓｔｆｕｒｎａｃｅｂｕｒｄｅｎｄｉｓｔｒｉｂｕｔｉｏｎ［Ｊ］．ＭａｔｅｒｉａｌｓａｎｄＭａｎｕ- ｆａｃｔｕｒｉｎｇＰｒｏｃｅｓｓｅｓ‚2003（18）：385－399．
［29］ 刘 臻．酒钢 1号高炉无钟炉顶布料实验研究 ［Ｄ］．东北大学大硕士学位论文‚2000．